![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ODP:
![]()

Zauważ, że aby równanie
![]() miało dwa rozwiązania dodatnie, to muszą być spełnione poniższe warunki:
miało dwa rozwiązania dodatnie, to muszą być spełnione poniższe warunki:
![]() – delta większa od zera
– delta większa od zera
![]() – iloczyn rozwiązań musi być większy od zera
– iloczyn rozwiązań musi być większy od zera
![]() – suma rozwiązań musi być większa od zera
– suma rozwiązań musi być większa od zera
Zacznij od pierwszego warunku i oblicz dla jakich
![]() delta będzie większa od zera.
delta będzie większa od zera.
![]()
![]()
![]()
Oblicz dla jakiego
![]() pierwsze równanie jest równe 0.
pierwsze równanie jest równe 0.
![]()
![]()
Oblicz dla jakiego
![]() drugie równanie jest równe 0.
drugie równanie jest równe 0.
![]()
![]()
![]()
![]()
![]()
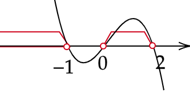
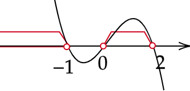
Zaznacz obliczone rozwiązania na osi i odczytaj przedziały, w których wykres jest nad osią.
![]()
Oblicz dla jakiego
![]() , iloczyn rozwiązań jest większy od zera. Skorzystaj ze wzorów Viete’a.
, iloczyn rozwiązań jest większy od zera. Skorzystaj ze wzorów Viete’a.
![]()
![]()
![]()
![]()
![]()
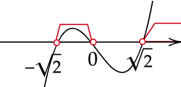
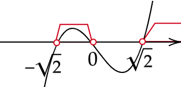
Zaznacz obliczone rozwiązania na osi i odczytaj przedziały, w których wykres jest nad osią.
![]()
Oblicz dla jakiego
![]() , suma rozwiązań jest większa od zera. Skorzystaj ze wzorów Viete’a.
, suma rozwiązań jest większa od zera. Skorzystaj ze wzorów Viete’a.
![]()
![]()
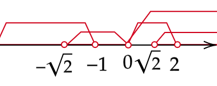
Zaznacz na osi wszystkie obliczone powyżej przedziały. Rozwiązaniem zadania, będzie wspólny przedział warunków zapisanych na początku.
![]()
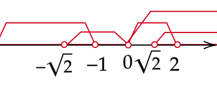
Oznacza, to że rozwiązanie
![]() ma dwa rozwiązania dodatnie dla
ma dwa rozwiązania dodatnie dla
![]() .
.