Matura z matematyki. Arkusz dodatkowy. Poziom rozszerzony. Czerwiec 2016

Arkusz egzaminacyjny, Wydawnictwo: CKE

Zadanie 14 - strona 14

Oblicz cosinusy kątów ostrych trójkąta prostokątnego, w których stosunek różnicy długości przyprostokątnych do długości przeciwprostokątnej wynosi $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$ – ponieważ cosinus musi być kątem ostrym

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

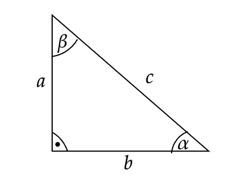
ODP: Cosinusy kątów ostrych trójkąta prostokątnego wynoszą $\text{[math]}$ oraz $\text{[math]}$

Wykonaj rysunek pomocniczy:

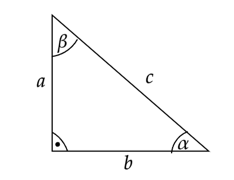
Zapisz warunek podany w treści zadania i rozbij lewą stronę na dwa ułamki.

$\text{[math]}$

$\text{[math]}$

Zauważ, że powstałe ułamki odpowiadają wartościom trygonometrycznych kąta $\text{[math]}$

$\text{[math]}$

Z powyższego równania wyznacz wartość sinusa.

$\text{[math]}$

Skorzystaj ze wzoru na jedynkę trygonometryczną: $\text{[math]}$ i podstaw wyznaczoną powyżej wartość sinusa.

$\text{[math]}$

Z powstałego równania oblicz wartość cosinusa. Skorzystaj ze wzoru skróconego mnożenia na kwadrat sumy: $\text{[math]}$ i przenieś wszystkie wartości na lewą stronę równania.

$\text{[math]}$

$\text{[math]}$

Zastosuj podstawienie:

$\text{[math]}$ – ponieważ cosinus musi być kątem ostrym

$\text{[math]}$

Oblicz deltę i miejsca zerowe powyższego równania.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Wróć z podstawieniem.

$\text{[math]}$

Oznacza to, że $\text{[math]}$ .

Zauważ, że cosinus i sinus dwóch różnych kątów ostrych w trójkącie prostokątnym jest sobie równy.

$\text{[math]}$

Na tej podstawie oblicz cosinus drugiego kąta ostrego tego trójkąta.

$\text{[math]}$

Więc $\text{[math]}$

Ćwiczenie 4, strona 10, Matematyka. Klasa 8. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 5.60, strona 143, Matematyka. Klasa 1. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 2, strona 98, Matematyka z plusem. Klasa 6. Zeszyt ćwiczeń. Wersja C – rozwiązania i odpowiedzi

Zadanie Co było na lekcji 7, strona 23, Matematyka. Klasa 5. Zeszyt ćwiczeń część 1 - rozwiązania i odpowiedzi.

Zadanie 6, strona 110, Matematyka. Klasa 2. Zbiór zadań. Poziom podstawowy – rozwiązania i odpowiedzi

Zadanie 3, strona 64, Matematyka z kluczem. Klasa 4. Podręcznik. Część 1 - rozwiązania i odpowiedzi

Zadanie 1, strona 81, MATeMAtyka. Klasa 1. Zbiór zadań. Zakres podstawowy – rozwiązania i odpowiedzi

Zadanie otwarte 5, strona 67, Matematyka wokół nas. Klasa 5. Zbiór zadań – rozwiązania i odpowiedzi

Ćwiczenie 4, strona 134, Matematyka z kluczem. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 3.29., strona 50, Matematyka. Klasa 3. Zbiór zadań. Zakres podstawowy - rozwiązania i odpowiedzi

2

2

2

2

2

4

4

5

6

8

10

11

12

14

16

18

20

Pełny spis treści