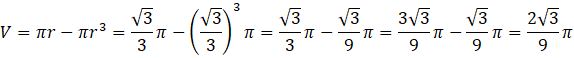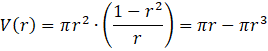
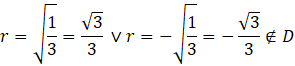
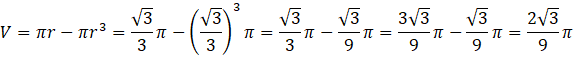
Oblicz największą objętość walca oraz promień podstawy, jeśli jego pole powierzchni całkowitej wynosi $\text{[math]}$

$\text{[math]}$

ODP: Największa objętość walca wynosi $\text{[math]}$

Zapisz wzór na pole całkowite walca.

$\text{[math]}$

Z powyższego równania wyznacz wartość $\text{[math]}$ , czyli wysokości walca.

$\text{[math]}$

Zauważ, że obie wielkości, czyli promień i wysokość muszą być większe od zera.

$\text{[math]}$

Zapisz dziedzinę równania, czyli przedział spełniający powyższe nierówności.

$\text{[math]}$

Zapisz wzór na objętość walca.

$\text{[math]}$

Pod powyższe równanie podstaw wyznaczoną wartość $\text{[math]}$ . Zauważ, że powstanie funkcja zmiennej $\text{[math]}$ Zapisz jej wzór w najprostszej postaci.

$\text{[math]}$

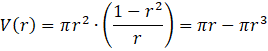
Oblicz pochodną funkcji $\text{[math]}$

$\text{[math]}$

Oblicz miejsca zerowe powstałej pochodnej, czyli przyrównaj jej wartość do zera.

$\text{[math]}$

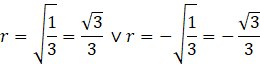
Zauważ, że $\text{[math]}$ nie należy do dziedziny.

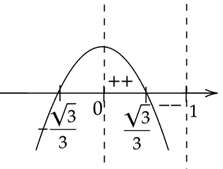
Zaznacz obliczone rozwiązania na osi. Ramiona paraboli skieruj do dołu ponieważ współczynnik stojący przy $\text{[math]}$ z największą potęgą jest ujemny. Pamiętaj o uwzględnieniu dziedziny.

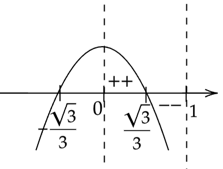
Oznacza to, że pochodna w przedziale $\text{[math]}$ ma jedno miejsce zerowe $\text{[math]}$ i zmienia w tym punkcie znak z dodatniego na ujemny. W takim razie funkcja $\text{[math]}$ rośnie do $\text{[math]}$ i potem maleje. Będzie to więc największa wartość pochodnej i funkcji.