W tym zadaniu musisz obliczyć sinus kąta pomiędzy prostą AE a płaszczyzną (ABCD), jeśli w sześcianie ABCDA1B1C1D1 punkt E jest punktem przecięcia się przekątnych kwadratu DCC1D1.
Określmy punkty:
F – środek odcinka AB
G – środek odcinka DC
Oraz:
a – długość boku sześcianu ABCDA1B1C1D1
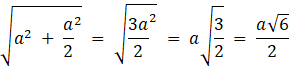
Trójkąt EFG jest trójkątem prostokątnym o bokach długości: a,
![]() ,
,
![]() .
.
A więc:
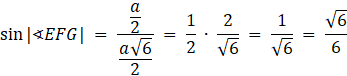

Określ, gdzie będzie znajdować się kąt nachylenia prostej AE do płaszczyzny (ABCD). Wyznacz długość boków powstałego trójkąta:
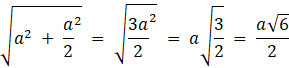
Oblicz sinus danego kąta:
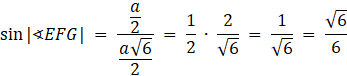

Ćwiczenie 2.
221Ćwiczenie 6.
225Zadanie 4.
228Ćwiczenie 1.
230Zadanie 2.
235Zadanie 4.
251Zadanie 1.
255Zadanie 2.
255Zadanie 3.
255Zadanie 5.
255Ćwiczenie 2.
260Zadanie 1.
264Zadanie 4.
264Zadanie 6.
265Zadanie 7.
265Ćwiczenie 4.
273Zadanie 1.
276Zadanie 2.
277Zadanie 4.
277Zadanie 5.
277Zadanie 6.
277Zadanie 8.
277Zadanie 9.
278Zadanie 10.
278Zadanie 12.
278Ćwiczenie 2.
281Zadanie 1.
282Zadanie 4.
283Zadanie 5.
293Zadanie 7.
293Zadanie 10.
293Zadanie 12.
294Zadanie 1.
298Zadanie 2.
298Zadanie 4.
305Zadanie 6.
306Zadanie 9.
306Zadanie 11.
307Zadanie 10.
309Zadanie 11.
309Zadanie 14.
309Zadanie 15.
309Zadanie 16.
310Zadanie 17.
310Zadanie 19.
310
