W tym zadaniu musisz obliczyć objętość graniastosłupa prawidłowego trójkątnego, jeśli kąt nachylenia przekątnej jego ściany bocznej do sąsiedniej ściany bocznej jest równy 30°, a pole przekroju płaszczyzną zawierającą przekątną ściany bocznej i wysokość podstawy jest równe 6√3.
Przekrój jest trójkątem o kątach 30°, 60° i 90°. Jeśli oznaczymy krawędź podstawy graniastosłupa jako a, to wysokość podstawy wynosi
![]() , a druga przyprostokątna ma miarę
, a druga przyprostokątna ma miarę
![]() .
.
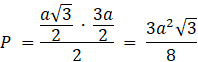
![]()
![]()
![]()
Obliczamy wysokość graniastosłupa:
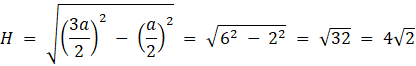
Obliczamy objętość:
![]()

Przekrój jest trójkątem o kątach 30°, 60° i 90°. Jeśli oznaczysz krawędź podstawy graniastosłupa jako a, to wysokość podstawy wynosi
![]() , a druga przyprostokątna ma miarę
, a druga przyprostokątna ma miarę
![]() . Wyznacz a:
. Wyznacz a:
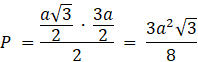
![]()
![]()
![]()
Oblicz wysokość graniastosłupa:
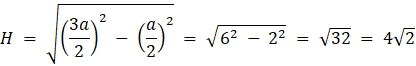
Oblicz objętość:
![]()

Ćwiczenie 2.
221Ćwiczenie 6.
225Zadanie 4.
228Ćwiczenie 1.
230Zadanie 2.
235Zadanie 4.
251Zadanie 1.
255Zadanie 2.
255Zadanie 3.
255Zadanie 5.
255Ćwiczenie 2.
260Zadanie 1.
264Zadanie 4.
264Zadanie 6.
265Zadanie 7.
265Ćwiczenie 4.
273Zadanie 1.
276Zadanie 2.
277Zadanie 4.
277Zadanie 5.
277Zadanie 6.
277Zadanie 8.
277Zadanie 9.
278Zadanie 10.
278Zadanie 12.
278Ćwiczenie 2.
281Zadanie 1.
282Zadanie 4.
283Zadanie 5.
293Zadanie 7.
293Zadanie 10.
293Zadanie 12.
294Zadanie 1.
298Zadanie 2.
298Zadanie 4.
305Zadanie 6.
306Zadanie 9.
306Zadanie 11.
307Zadanie 10.
309Zadanie 11.
309Zadanie 14.
309Zadanie 15.
309Zadanie 16.
310Zadanie 17.
310Zadanie 19.
310
