W tym zadaniu musisz wykazać, że tg α : tg β = a : b, jeśli podstawą ostrosłupa jest równoległobok o bokach długości a i b, spodek wysokości ostrosłupa to punkt przecięcia się przekątnych tego równoległoboku, α oznacza kąt między płaszczyzną podstawy a ścianą boczną, zawierającą bok równoległoboku o długości a, zaś β — kąt między płaszczyzną podstawy a ścianą boczną zawierającą bok równoległoboku o długości b.
Oznaczamy wysokość ostrosłupa jako H. Korzystając z tego, że równoległobok można podzielić na 4 równoległoboki przystające o bokach dwa razy krótszych niż równoległobok, którego boki mają długość a i b, zapisujemy:
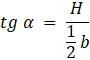
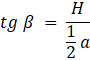
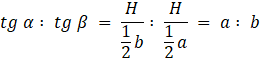
Co należało wykazać.

Wyznacz
![]() , a następnie je porównaj:
, a następnie je porównaj:
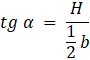
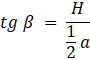
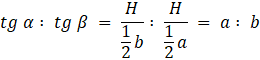

Ćwiczenie 2.
221Ćwiczenie 6.
225Zadanie 4.
228Ćwiczenie 1.
230Zadanie 2.
235Zadanie 4.
251Zadanie 1.
255Zadanie 2.
255Zadanie 3.
255Zadanie 5.
255Ćwiczenie 2.
260Zadanie 1.
264Zadanie 4.
264Zadanie 6.
265Zadanie 7.
265Ćwiczenie 4.
273Zadanie 1.
276Zadanie 2.
277Zadanie 4.
277Zadanie 5.
277Zadanie 6.
277Zadanie 8.
277Zadanie 9.
278Zadanie 10.
278Zadanie 12.
278Ćwiczenie 2.
281Zadanie 1.
282Zadanie 4.
283Zadanie 5.
293Zadanie 7.
293Zadanie 10.
293Zadanie 12.
294Zadanie 1.
298Zadanie 2.
298Zadanie 4.
305Zadanie 6.
306Zadanie 9.
306Zadanie 11.
307Zadanie 10.
309Zadanie 11.
309Zadanie 14.
309Zadanie 15.
309Zadanie 16.
310Zadanie 17.
310Zadanie 19.
310
