W tym zadaniu musisz obliczyć długości wszystkich krawędzi ostrosłupa, którego podstawą jest trapez prostokątny o obwodzie równym 50, jeśli wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod takim kątem α, że tg α = 2,5, a wysokość ostrosłupa jest równa 15.
![]()
![]()
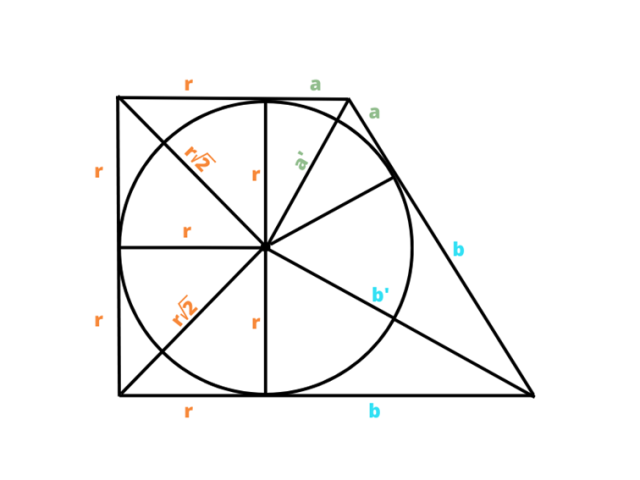
Korzystając z tego, że r = 6, zapisujemy:
![]()
![]()
![]()
Oraz:
![]()
![]()
![]()
![]()
![]()
Długości krawędzi podstawy to: 10, 12, 13, i 15.
![]()
![]()
![]()
![]()
![]()
![]()
Długości krawędzi bocznych to:
![]()

Skorzystaj z własności czworokąta, w który wpisano okrąg i twierdzenia Pitagorasa. Oznacz odcinki jak na rysunku, korzystając z zależności okręgu wpisanego, oblicz promień okręgu i długości krawędzi podstaw:
![]()
![]()
Korzystając z tego, że r = 6, zapisujemy:
![]()
![]()
![]()
Oraz:
![]()
![]()
![]()
![]()
![]()
Na koniec oblicz długość krawędzi bocznych:
![]()
![]()
![]()
![]()
![]()
![]()

Ćwiczenie 2.
221Ćwiczenie 6.
225Zadanie 4.
228Ćwiczenie 1.
230Zadanie 2.
235Zadanie 4.
251Zadanie 1.
255Zadanie 2.
255Zadanie 3.
255Zadanie 5.
255Ćwiczenie 2.
260Zadanie 1.
264Zadanie 4.
264Zadanie 6.
265Zadanie 7.
265Ćwiczenie 4.
273Zadanie 1.
276Zadanie 2.
277Zadanie 4.
277Zadanie 5.
277Zadanie 6.
277Zadanie 8.
277Zadanie 9.
278Zadanie 10.
278Zadanie 12.
278Ćwiczenie 2.
281Zadanie 1.
282Zadanie 4.
283Zadanie 5.
293Zadanie 7.
293Zadanie 10.
293Zadanie 12.
294Zadanie 1.
298Zadanie 2.
298Zadanie 4.
305Zadanie 6.
306Zadanie 9.
306Zadanie 11.
307Zadanie 10.
309Zadanie 11.
309Zadanie 14.
309Zadanie 15.
309Zadanie 16.
310Zadanie 17.
310Zadanie 19.
310
