W tym zadaniu musisz obliczyć pole powierzchni całkowitej graniastosłupa prostego, którego podstawą jest trapez równoramienny o kącie ostrym równym 60°, jeśli rzut prostokątny przekątnej graniastosłupa na płaszczyznę podstawy zawiera się w dwusiecznej kąta ostrego trapezu i ma długość
![]() , a dwusieczna kąta ostrego trapezu tworzy z przekątną graniastosłupa kąt o mierze 30°
, a dwusieczna kąta ostrego trapezu tworzy z przekątną graniastosłupa kąt o mierze 30°
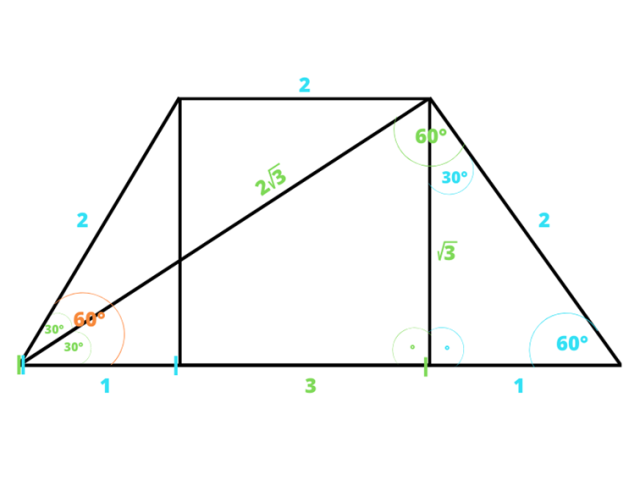
Korzystając z własności trójkąta 30°, 60°, 90° obliczamy długość poszczególnych odcinków jak na rysunku wyżej. Następnie obliczamy:
![]()
![]()
![]()

Korzystając z własności trójkąta 30°, 60°, 90° oblicz długość poszczególnych odcinków jak na rysunku wyżej. Następnie oblicz pola:
![]()
![]()
![]()

Ćwiczenie 2.
221Ćwiczenie 6.
225Zadanie 4.
228Ćwiczenie 1.
230Zadanie 2.
235Zadanie 4.
251Zadanie 1.
255Zadanie 2.
255Zadanie 3.
255Zadanie 5.
255Ćwiczenie 2.
260Zadanie 1.
264Zadanie 4.
264Zadanie 6.
265Zadanie 7.
265Ćwiczenie 4.
273Zadanie 1.
276Zadanie 2.
277Zadanie 4.
277Zadanie 5.
277Zadanie 6.
277Zadanie 8.
277Zadanie 9.
278Zadanie 10.
278Zadanie 12.
278Ćwiczenie 2.
281Zadanie 1.
282Zadanie 4.
283Zadanie 5.
293Zadanie 7.
293Zadanie 10.
293Zadanie 12.
294Zadanie 1.
298Zadanie 2.
298Zadanie 4.
305Zadanie 6.
306Zadanie 9.
306Zadanie 11.
307Zadanie 10.
309Zadanie 11.
309Zadanie 14.
309Zadanie 15.
309Zadanie 16.
310Zadanie 17.
310Zadanie 19.
310
