W tym zadaniu musisz wykazać, że jeśli α jest kątem nachylenia płaszczyzny przekroju do płaszczyzny podstawy, a 2β jest kątem ostrym rombu, to cos α = tg β, jeśli podstawą prostopadłościanu ABCDA1B1C1D1 jest kwadrat ABCD, punkty E, F są odpowiednio środkami krawędzi BB1 i DD1 i przez punkty A, E, C1, F poprowadzono płaszczyznę przekroju.
Oznaczmy: a – długość krawędzi podstawy, H – wysokość prostopadłościanu
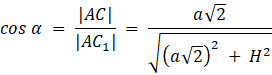
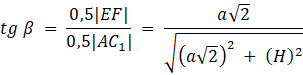
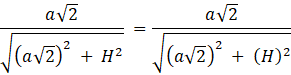
Co należało wykazać.

Wykaż, że cos α = tg β:
Oznacz: a – długość krawędzi podstawy, H – wysokość prostopadłościanu
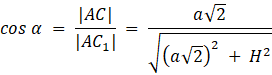
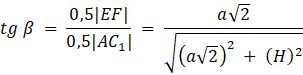
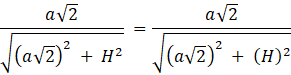

Ćwiczenie 2.
221Ćwiczenie 6.
225Zadanie 4.
228Ćwiczenie 1.
230Zadanie 2.
235Zadanie 4.
251Zadanie 1.
255Zadanie 2.
255Zadanie 3.
255Zadanie 5.
255Ćwiczenie 2.
260Zadanie 1.
264Zadanie 4.
264Zadanie 6.
265Zadanie 7.
265Ćwiczenie 4.
273Zadanie 1.
276Zadanie 2.
277Zadanie 4.
277Zadanie 5.
277Zadanie 6.
277Zadanie 8.
277Zadanie 9.
278Zadanie 10.
278Zadanie 12.
278Ćwiczenie 2.
281Zadanie 1.
282Zadanie 4.
283Zadanie 5.
293Zadanie 7.
293Zadanie 10.
293Zadanie 12.
294Zadanie 1.
298Zadanie 2.
298Zadanie 4.
305Zadanie 6.
306Zadanie 9.
306Zadanie 11.
307Zadanie 10.
309Zadanie 11.
309Zadanie 14.
309Zadanie 15.
309Zadanie 16.
310Zadanie 17.
310Zadanie 19.
310
