W tym zadaniu musisz wykazać, że jeśli pole przekroju jest równe P, a objętość ostrosłupa jest równa V, to długość krawędzi podstawy jest równa
![]() , jeśli podstawą ostrosłupa jest romb, wszystkie jego ściany boczne są nachylone do płaszczyzny podstawy pod tym samym kątem oraz ostrosłup przecięto płaszczyzną prostopadłą do dwóch przeciwległych ścian bocznych i zawierającą wysokość tego ostrosłupa.
, jeśli podstawą ostrosłupa jest romb, wszystkie jego ściany boczne są nachylone do płaszczyzny podstawy pod tym samym kątem oraz ostrosłup przecięto płaszczyzną prostopadłą do dwóch przeciwległych ścian bocznych i zawierającą wysokość tego ostrosłupa.
W romb można wpisać okręg o promieniu r. Wówczas:
![]()
![]()
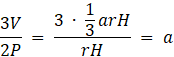
Co kończy dowód.

Wyznacz pole przekroju:
![]()
Wyznacz objętość ostrosłupa:
![]()
Oblicz
![]() :
:
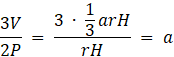

Ćwiczenie 2.
221Ćwiczenie 6.
225Zadanie 4.
228Ćwiczenie 1.
230Zadanie 2.
235Zadanie 4.
251Zadanie 1.
255Zadanie 2.
255Zadanie 3.
255Zadanie 5.
255Ćwiczenie 2.
260Zadanie 1.
264Zadanie 4.
264Zadanie 6.
265Zadanie 7.
265Ćwiczenie 4.
273Zadanie 1.
276Zadanie 2.
277Zadanie 4.
277Zadanie 5.
277Zadanie 6.
277Zadanie 8.
277Zadanie 9.
278Zadanie 10.
278Zadanie 12.
278Ćwiczenie 2.
281Zadanie 1.
282Zadanie 4.
283Zadanie 5.
293Zadanie 7.
293Zadanie 10.
293Zadanie 12.
294Zadanie 1.
298Zadanie 2.
298Zadanie 4.
305Zadanie 6.
306Zadanie 9.
306Zadanie 11.
307Zadanie 10.
309Zadanie 11.
309Zadanie 14.
309Zadanie 15.
309Zadanie 16.
310Zadanie 17.
310Zadanie 19.
310
