Opracowania zadań z podręczników
Matura z matematyki. Poziom rozszerzony. 2022
Podpunkt c)

Arkusz egzaminacyjny, Wydawnictwo: CKE

Zadanie 15, c) - strona 22

Oblicz dla jakiej długości boków trójkąta jego pole jest największe.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

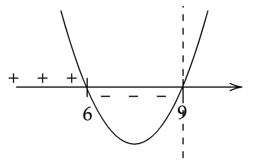
$\text{[math]}$ - największa wartość pochodnej.

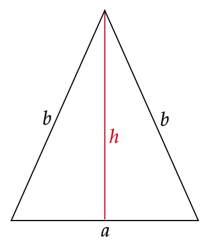
Oblicz długości boków, dla których pole jest największe.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Przekształć licznik ułamka, aby całe wyrażenie znalazło się pod pierwiastkiem.

$\text{[math]}$

Zapisz funkcję pomocniczą zmiennej b. Skorzystaj z wartości pod pierwiastkiem.

$\text{[math]}$

Oblicz pochodną funkcji.

$\text{[math]}$

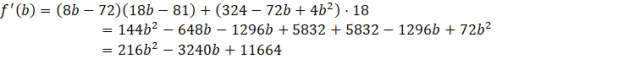
Zauważ, że powstało równanie kwadratowe.

$\text{[math]}$

$\text{[math]}$

Oblicz deltę i miejsca zerowe.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

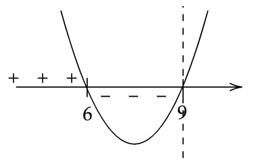
Oznacza to, że pochodna w przedziale $\text{[math]}$ ma jedno miejsce zerowe b=6 i zmienia w tym punkcie znak z dodatniego na ujemny. W takim razie funkcja $\text{[math]}$ (oraz $\text{[math]}$ ) rośnie w przedziale $\text{[math]}$ ,a maleje w przedziale $\text{[math]}$ . Więc będzie do największa wartość pochodnej.

Oblicz długość boków dla których pole będzie największe.

$\text{[math]}$

$\text{[math]}$ – trójkąt równoboczny

Zadanie 12., strona 127, Matematyka. Klasa 1. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie 7, strona 61, Matematyka z kluczem. Klasa 5. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 4.1., strona 339, Prosto do matury. Matematyka. Klasa 2. Podręcznik. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie 4, strona 24, Matematyka. Klasa 7. Ćwiczenia - rozwiązania i odpowiedzi.

Zadanie 13, strona 53, Matematyka. Klasa 5. Zeszyt ćwiczeń część 1 - rozwiązania i odpowiedzi.

Zadanie 1, strona 6, Matematyka wokół nas. Klasa 7. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 28, strona 71, Matematyka z plusem. Klasa 6. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 29., strona 391, Prosto do matury. Matematyka. Klasa 1. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 3.4., strona 413, Prosto do matury. Matematyka. Klasa 1. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 4.16, strona 79, Matematyka. Klasa 2. Zbiór zadań. Poziom podstawowy – rozwiązania i odpowiedzi

2

2

2

2

4

5

6

8

10

12

14

16

18

20

Zadanie 15

22

22

22

22

Pełny spis treści