Musisz obliczyć długość krawędzi bocznych ostrosłupa.
Zauważamy, że jedną z krawędzi bocznych ostrosłupa jest jego wysokość. Zatem wynosi ona 8.
Dwoma kolejnymi jego krawędziami są przekątne ścian bocznych, które obliczymy z twierdzenia Pitagorasa.
62 + 82 = c2
36 + 64 = c2
c2 = 100
c = 10
Czwartą krawędzią boczną ostrosłupa jest przekątna graniastosłupa. Obliczymy ją z twierdzenia Pitagorasa, gdzie przyprostokątnymi będą przekątna podstawy, czyli kwadratu oraz wysokość graniastosłupa, natomiast przeciwprostokątną będzie przekątna graniastosłupa.
Przekątna kwadratu:
a![]()
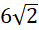
(![]()
72 + 64 = d2
d2 = 136
d = ![]()
![]()
Długości krawędzi wynoszą: 8, 10, 10 i 2![]()

Twierdzenie Pitagorasa: Jeżeli trójkąt jest prostokątny to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.
a2 + b2 = c2

Zadanie B
168Zadanie 1
170Zadanie 3
170Zadanie 5
171Zadanie 7
171Zadanie 12
172Zadanie 13
172Zadanie 14
172Zadanie 16
172Ćwiczenie B
174Zadanie 1
175Zadanie 2
175Zadanie 5
176Zadanie 6
176Zadanie 7
176Zadanie 8
176Zadanie 11
177Ćwiczenie B
181Zadanie 1
181Zadanie 2
182Zadanie 3
182Zadanie 4
182Zadanie 5
182Zadanie 7
183Zadanie 8
183Zadanie 3
186Zadanie 4
186Zadanie 5
186Zadanie 1
189Zadanie 2
189Zadanie 4
189Zadanie 10
190Ćwiczenie B
193Zadanie 7
195Zadanie 9
195Zadanie 12
196Zadanie 15
197Zadanie 3
200Zadanie 6
200Zadanie 9
200Zadanie 12
201Zadanie 14
201Zadanie 15
201Zadanie 16
201Zadanie 18
201Zadanie 24
202Zadanie 27
202Zadanie 30
203Zadanie 31
203Zadanie 33
203Zadanie 34
203Zadanie 38
204Zadanie 39
204
