W tym zadaniu musisz uzupełnić wzory funkcji oraz opisy przesunięcia, a następnie narysować wykres funkcji $\text{[math]}$ i podać współrzędne jej wierzchołka.

$\text{[math]}$

przesuwamy wykres o 2 jednostki w lewo i o 3 jednostki do góry

$\text{[math]}$

Współrzędne wierzchołka wykresu funkcji $\text{[math]}$ : $\text{[math]}$

Współczynnik a jest taki sam zarówno we wzorze funkcji kwadratowej w postaci ogólnej, jak i w kanonicznej. Jeśli funkcja przed przesunięciem ma postać $\text{[math]}$ to znaczy, że współczynniki b oraz c wynoszą 0, ten sam współczynnik a pojawia się w postaci kanonicznej: $\text{[math]}$

Uzupełnij wzór $\text{[math]}$ o współczynnik $\text{[math]}$ .

Następnie wiedząc, że funkcja została przesunięta o 2 jednostki w lewo i o 3 jednostki do góry uzupełnij wykres funkcji po przesunięciu. Skorzystaj z poniższych informacji.

Po przesunięciu funkcji wzdłuż osi OY o q jednostek ( $\text{[math]}$ ) wzór funkcji $\text{[math]}$ zmienia się następująco:

Przesunięcie w górę: $\text{[math]}$

Przesunięcie w dół: $\text{[math]}$

Po przesunięciu funkcji wzdłuż osi OX o p jednostek ( $\text{[math]}$ ) wzór funkcji $\text{[math]}$ zmienia się następująco:

Przesunięcie w prawo: $\text{[math]}$

Przesunięcie w lewo: $\text{[math]}$

Po uzupełnieniu wzoru $\text{[math]}$ odczytaj współrzędne wierzchołka, z postaci kanonicznej funkcji, wiedząc, że wierzchołek znajduje się w punkcie: $\text{[math]}$ .

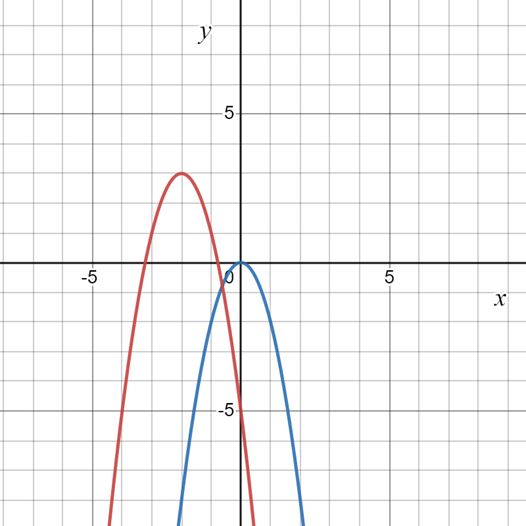
Na koniec narysuj funkcję $\text{[math]}$ w układzie współrzędnych. Aby narysować wykres przesuniętej funkcji, zaznacz punkty charakterystyczne np. punkty przecięcia z osiami układu i połącz je. W rozwiązaniu funkcja narysowana kolorem czerwonym to funkcja po przesunięciu, którą musisz dorysować, a funkcja niebieska to ta, która jest już narysowana w ćwiczeniach.