W tym zadaniu musisz wykazać, jaki prostokąt o polu równym 4 ma najmniejszy obwód.
Pole prostokąta wyraża wzór ![]()
![]()
Dodatkowo wzór na obwód wyraża się jako ![]()
![]()
Wstawmy równanie na pole w postaci ![]()
![]()
Szkicując tę funkcję, otrzymamy argument (a), dla którego obwód jest minimalny:
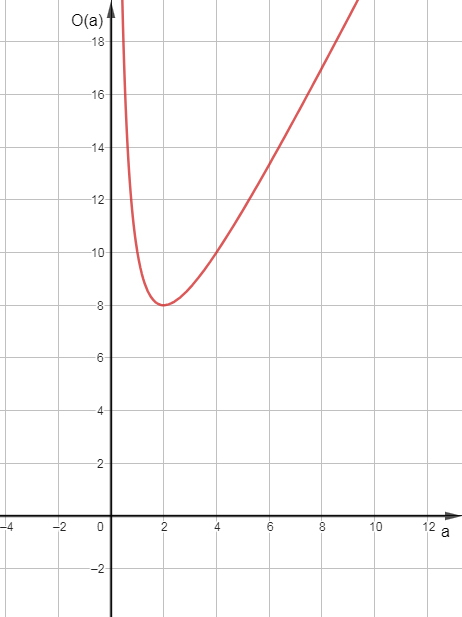

Wypisz wyrażenia na obwód i pole dowolnego prostokąta. Potraktuj obwód jako funkcję jednego z boków i podstaw za drugi bok jego wartość z wyrażenia na pole. Szkicując wykres obwodu uzyskasz minimum.

Zadanie 1.
120Zadanie 2.
121Zadanie 3.
121Zadanie 4.
121Zadanie 6.
121Zadanie 7.
122Zadanie 8.
122Zadanie 3.
126Zadanie 4.
126Zadanie 5.
126Zadanie 1.
132Zadanie 2.
133Zadanie 3.
133Zadanie 4.
133Zadanie 1.
136Zadanie 2.
136Zadanie 3.
137Zadanie 4.
137Zadanie 5.
137Zadanie 6.
137Zadanie 7.
137Zadanie 8.
137Zadanie 9.
137Zadanie 1.
142Zadanie 2.
142Zadanie 3.
143Zadanie 4.
143Zadanie 5.
143Zadanie 8.
143Zadanie 1.
149Zadanie 2.
149Zadanie 3.
149Zadanie 5.
149Zadanie 3.
159Zadanie 4.
159Ćwiczenie 1.
161Ćwiczenie 2.
162Ćwiczenie 3.
163Zadanie 1.
171Zadanie 2.
171Zadanie 3.
171Zadanie 4.
172Zadanie 5.
172Zadanie 6.
172Zadanie 7.
172Zadanie 1.
177Zadanie 2.
178Zadanie 3.
178Zadanie 4.
178Zadanie 5.
178Zadanie 6.
178Zadanie 10.
180Zadanie 11.
180
