W tym zadaniu oblicz długości boków tego trójkąta, jeżeli jego obwód wynosi 72,8 cm, wiedząc, że w trójkącie różnobocznym średni bok jest o 20% dłuższy od najkrótszego oraz stanowi długości boku najdłuższego.
1 bok: x
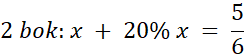
3 bok: y
Obw. = 72,8 cm = x + (x + 20% x) + y
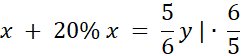

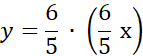
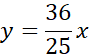
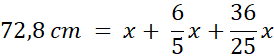
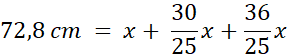
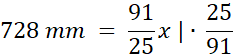
x = 8 ∙ 25 mm = 200 mm = 20 cm
Odp.
1 bok: x = 20 cm
2 bok: x + 20% x = 20 cm + 20% ∙ 20 cm = 20 cm + 4 cm = 24 cm
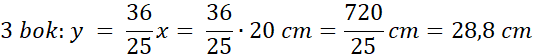

Znasz zależności wszystkich boków trójkąta. Możesz więc zapisać, że obwód jest równy:
Obw. = 72,8 cm = x + (x + 20% x) + y.
Najpierw pozbądź się jednej niewiadomej – przelicz długość 3. boku na x.
Następnie podstaw długości boków z niewiadomą x do wzoru na obwód trójkąta.
Ze wzoru możesz wyliczyć x, czyli długość najkrótszego boku. Na tej podstawie wyliczysz długości kolejnych boków.

Zadanie 4.
40Zadanie 7.
40Zadanie 8.
40Zadanie 9.
40Zadanie 10.
41Zadanie 11.
41Zadanie 2.
42Zadanie 3.
42Zadanie 6.
42Zadanie 10.
43Zadanie 11.
43Zadanie 1.
43Zadanie 2.
43Zadanie 5.
43Zadanie 6.
43Zadanie 8.
44Zadanie 9.
44Zadanie 10.
44Zadanie 1.
45Zadanie 3.
46Zadanie 6.
46Zadanie 7.
46Zadanie 9.
47Zadanie 15.
47Zadanie 16.
47Zadanie 20.
48Zadanie 23.
48Zadanie 24.
49Zadanie 25.
49Zadanie 1.
50Zadanie 2.
50
