Zapisz wzór funkcji
w postaci kanonicznej i ogólnej, jeśli jej zbiorem wartości jest przedział
oś symetrii opisana jest równaniem
, a do wykresu paraboli należy punkt P(-1,-4).
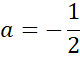
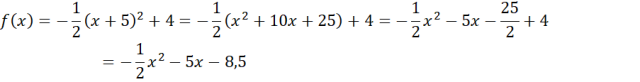
Skorzystaj z tego, że jeśli osią symetrii paraboli jest
, to pierwszą współrzędną wierzchołka jest (-5). A jeśli jej zbiorem wartości jest przedział
to liczba 4 jest drugą współrzędną wierzchołka.
Zauważ, że funkcja kwadratowa w postaci kanonicznej wyraża się wzorem:
, gdzie
to współrzędne wierzchołka paraboli. Podstaw współrzędne wierzchołka oraz punktu P pod powyższy wzór funkcji i z powstałego równania wyznacz wartość
.
Na koniec zapisz wzór szukanej funkcji w postaci kanonicznej, a następnie doprowadź ją do postaci ogólnej. Zauważ wzór skróconego mnożenia na kwadrat sumy:
i dokonaj redukcji wyrazów podobnych,