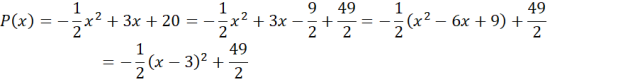
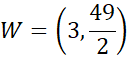
Parabola ma ramiona skierowane do dołu ponieważ współczynnik kierunkowy
![]() jest ujemny, więc największą wartość osiąga w wierzchołku.
jest ujemny, więc największą wartość osiąga w wierzchołku.
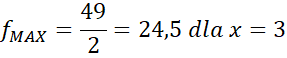

Na podstawie podpunktu a) znasz wzór funkcji
![]() w postaci ogólnej.
w postaci ogólnej.
Zauważ, że funkcja kwadratowa w postaci kanonicznej wyraża się wzorem:
![]() , gdzie
, gdzie
![]() to współrzędne wierzchołka paraboli. Liczbę 20 zapisz w postaci sumy liczb
to współrzędne wierzchołka paraboli. Liczbę 20 zapisz w postaci sumy liczb
![]() i
i
![]() , następnie zauważ wzór skróconego mnożenia na kwadrat różnicy:
, następnie zauważ wzór skróconego mnożenia na kwadrat różnicy:
![]() . Z powstałego wzoru wyznacz współrzędne wierzchołka tej paraboli.
. Z powstałego wzoru wyznacz współrzędne wierzchołka tej paraboli.
Zauważ, że największa wartość funkcji znajduję się w wierzchołku. Więc największe pole będzie drugą współrzędną wierzchołka, a
![]() dla którego jest ono przyjmowane będzie jego pierwsza współrzędną
dla którego jest ono przyjmowane będzie jego pierwsza współrzędną