Zapisz wzór funkcji
w postaci kanonicznej, podaj przedziały monotoniczności oraz wyznacz miejsca zerowe.
Funkcja jest malejąca dla
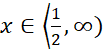
Funkcja jest rosnąca dla
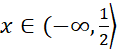
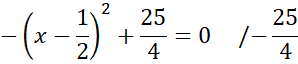
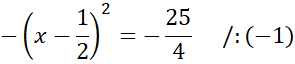
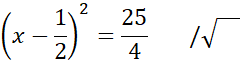
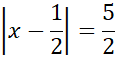
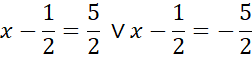
Zauważ, że funkcja kwadratowa w postaci kanonicznej wyraża się wzorem:
, gdzie
to współrzędne wierzchołka paraboli. Liczbę 6 zapisz w postaci sumy liczb
i
, następnie zauważ wzór skróconego mnożenia na kwadrat różnicy:
.
Parabola ma ramiona skierowane do dołu ponieważ współczynnik kierunkowy
jest ujemny, więc wykres funkcji będzie rosnący aż do wierzchołka i malejący od niego.
Zauważ, że miejsce zerowe funkcji można obliczyć rozwiązując równanie
. Aby to zrobić przyrównaj wzór funkcji
do zera i z powstałego równania wyznacz
.
Zauważ, że równanie z wartością bezwzględną:
możesz zapisać jako dwa równania:
.