Wykonaj wykres funkcji
i omów jej własności.
| -2 | -1 | 0 | 1 | 2 |
| -12 | -3 | 0 | -3 | -12 |
·
·
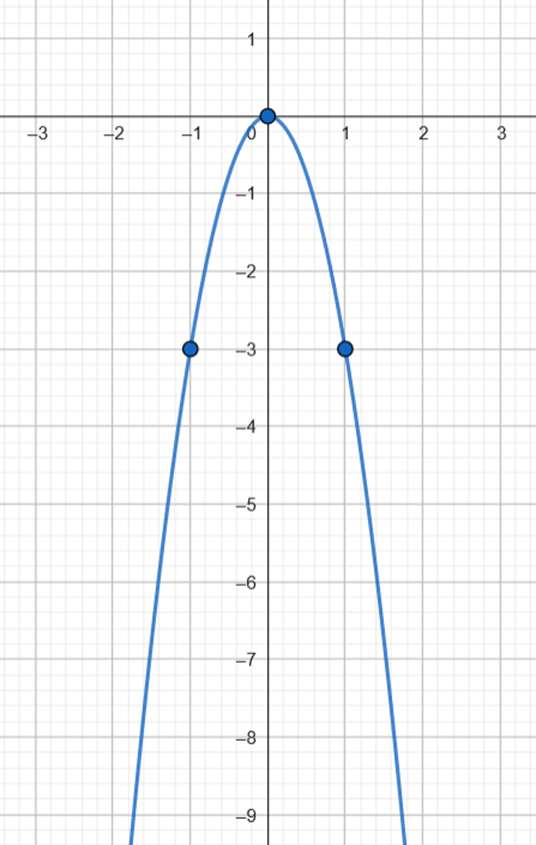
· Wierzchołek w punkcie (0,0)
· Miejsce zerowe:
·
dla
· Funkcja maleje dla
Funkcja rośnie dla
· Ramiona paraboli są skierowane do dołu.
· Funkcja nie jest różnowartościowa
· Funkcja przyjmuje wartość największą
dla
.
Funkcja nie przyjmuje wartości najmniejszej.
· Osią symetrii paraboli jest prosta o równaniu
.
Narysuj tabelę, w miejsce
wstaw dowolne liczby rzeczywiste, a w miejsce
wartość funkcji dla zapisanych argumentów. Aby to obliczyć w miejsce
we wzorze funkcji
wstaw podane liczby i wyznacz ich wartości.
Zaznacz w układzie współrzędnych otrzymane punkty i przeprowadź parabolę przechodzącą przez nie.
Następnie na podstawie wykresu odczytaj dziedzinę funkcji: przedział, do którego należą argumenty funkcji na osi OX oraz zbiór wartości: przedział, do którego należą wartości funkcji na osi OY. Następnie zapisz jej wierzchołek oraz miejsca zerowe funkcji
, czyli argumenty:
, dla których wykres przecina oś OX. Dodatkowo zapisz dla jakich argumentów wykres funkcji znajduję się nad oraz pod osią OX. Następnie odczytaj z wykresu argumenty, dla których wykres funkcji jest rosnący, a dla których malejący oraz dla jakich argumentów funkcja przyjmuje wartość największą i najmniejszą. Na koniec ustal, czy funkcja jest różnowartościowa, czyli czy dla dowolnego argumentu, żadna z wartości nie jest taka sama oraz zapisz równanie osi symetrii paraboli.