Matura z matematyki. Arkusz dodatkowy. Poziom rozszerzony. Czerwiec 2019

Arkusz egzaminacyjny, Wydawnictwo: CKE

Zadanie 12 - strona 12

Oblicz dla jakich wartości $\text{[math]}$ równanie $\text{[math]}$ ma dwa różne dodatnie rozwiązania $\text{[math]}$ , spełniające nierówność $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

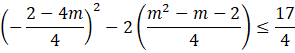
ODP: Wartości $\text{[math]}$ spełniające warunki zadania są w przedziale $\text{[math]}$

Zapisz warunki jakie muszą spełniać miejsca zerowe, aby każde z nich było dodatnie i różne od siebie:

$\text{[math]}$ – iloczyn musi być dodatni

$\text{[math]}$ – suma musi być dodatnia

$\text{[math]}$

$\text{[math]}$

Rozwiąż pierwszy warunek. Skorzystaj ze wzoru Viete’a.

$\text{[math]}$

$\text{[math]}$

Rozwiąż powstałą nierówność.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Rozwiąż drugi warunek. Ponownie skorzystaj ze wzoru Viete’a.

$\text{[math]}$

$\text{[math]}$

Rozwiąż powstałą nierówność.

$\text{[math]}$

$\text{[math]}$

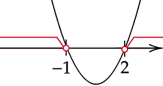
Oblicz deltę i miejsca zerowe.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Zaznacz uzyskane rozwiązania na osi i zapisz przedział, w którym parabola jest nad osią.

$\text{[math]}$

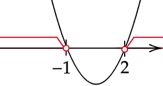
Rozwiąż trzeci warunek. Doprowadź lewą stronę nierówności do uzyskania postaci z wzorami Viete’a.

$\text{[math]}$

$\text{[math]}$

Rozwiąż powstałą nierówność.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

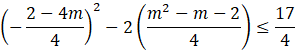
Oblicz deltę i miejsca zerowe.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Zaznacz uzyskane rozwiązania na osi i zapisz przedział, w którym parabola jest pod lub na osi.

$\text{[math]}$

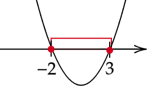
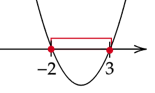
Zaznacz wszystkie wartości $\text{[math]}$ obliczone w każdym z warunków na osi. Rozwiązaniem zadania będzie ich wspólny przedział.

$\text{[math]}$

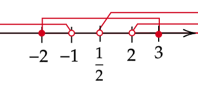
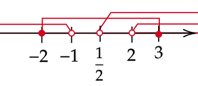
Oznacza to, że wartości $\text{[math]}$ spełniające warunki zadania znajdują się w przedziale $\text{[math]}$

Zadanie 54., strona 53, Matematyka z plusem. Klasa 4. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 1, strona 76, Matematyka z plusem. Klasa 5. Zeszyt Ćwiczeń – rozwiązania i odpowiedzi

Zadanie 3., strona 43, MATeMAtyka. Klasa 3. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 30., strona 250, MATeMAtyka. Klasa 1. Zbiór Zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie Wyzwanie, strona 230, Matematyka wokół nas. Klasa 7. Podręcznik - rozwiązania i odpowiedzi

Zadanie 8, strona 82, Matematyka z plusem. Klasa 6. Zeszyt ćwiczeń. Wersja C – rozwiązania i odpowiedzi

Zadanie 239, strona 111, Matematyka. Klasa 2. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 77., strona 229, Matematyka z plusem. Klasa 3. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie 8., strona 65, Matematyka z plusem. Klasa 6. Podręcznik - rozwiązania i odpowiedzi

Zadanie 6.1., strona 253, Prosto do matury. Klasa 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

2

2

2

2

4

5

6

7

8

9

10

12

14

16

18

Pełny spis treści