Udowodnij, że
![]() , jeśli w trójkącie ABC bok AB ma długość
, jeśli w trójkącie ABC bok AB ma długość
![]() oraz dane są długości środkowych AE i BD: |AE| = 6 cm, |BD| = 3 cm.
oraz dane są długości środkowych AE i BD: |AE| = 6 cm, |BD| = 3 cm.
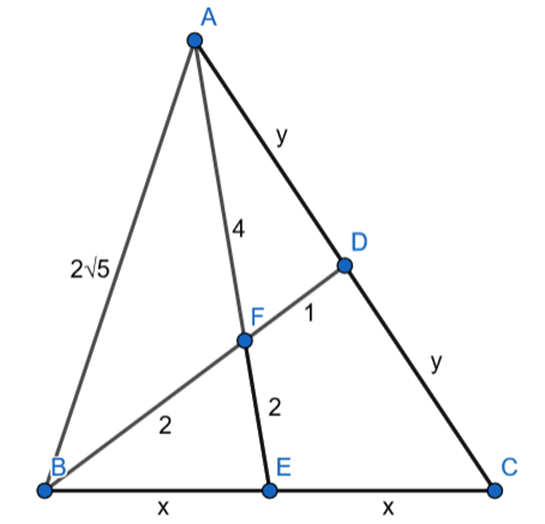
![]()
![]()
![]()
Trójkąt AFB jest prostokątny, więc proste AE i BD przecinają się pod kątem prostym.
Czyli
![]()
To kończy dowód.

Skorzystaj z tego, że środkową nazywany odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku, a środek ciężkości jest punktem przecięcia środkowych w trójkącie oraz dzieli on każdą ze środkowych w stosunku 2 : 1 licząc od wierzchołka.
Na tej podstawie wykonaj rysunek pomocniczy i skorzystaj z twierdzenia Pitagorasa, aby ustalić, czy proste AE i BD są prostopadłe.

Zadanie 1
272Zadanie 5
272Zadanie 6
272Zadanie 7
272Zadanie 8
272Zadanie 5
277Zadanie 6
277Zadanie 1
280Zadanie 2
281Zadanie 3
281Zadanie 4
281Zadanie 1
286Zadanie 2
287Zadanie 4
287Zadanie 5
287Zadanie 6
287Zadanie 7
287Zadanie 8
287Zadanie 9
287Zadanie 14
287Zadanie 2
291Zadanie 3
291Zadanie 4
291Zadanie 5
291Zadanie 1
298Zadanie 2
298Zadanie 5
298Zadanie 9
298Zadanie 10
298Zadanie 11
298Zadanie 1
302Zadanie 2
302Zadanie 9
303Zadanie 10
303Zadanie 11
303Zadanie 12
303Zadanie 1
309Zadanie 4
310Zadanie 5
310Zadanie 6
310Zadanie 7
310Zadanie 8
310Zadanie 9
310Zadanie 10
310Zadanie 11
310Zadanie 1
321Zadanie 2
321Zadanie 3
321Zadanie 4
322Zadanie 5
322Zadanie 6
322Zadanie 9
322Zadanie 10
329Zadanie 11
329Zadanie 15
329
