Narysuj konstruktywnie kąt o mierze
![]()
Zacznij od konstrukcji trójkąta równobocznego.
Narysuj odcinek AB.

Z punktu A zakreśl cyrklem łuk przechodzący przez punkt B.
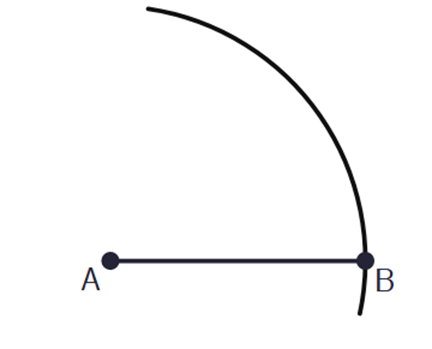
Podobnie postąp z punktem B i przechodzącym przez punkt A łukiem. Miejsce przecięcia łuków oznacz literą C.
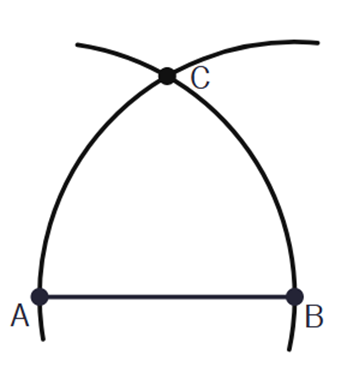
Z wierzchołków A i B poprowadź proste przechodzące przez punkt C. W ten sposób powstanie trójkąt równoboczny.
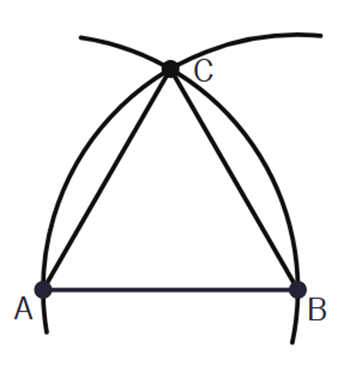
Zauważ, że wszystkie kąty w trójkącie równobocznym mają miarę
![]() . Skonstruuj dwusieczną jednego z jego kątów, aby uzyskać kąt o mierze
. Skonstruuj dwusieczną jednego z jego kątów, aby uzyskać kąt o mierze
![]() .
.
Dwusieczna kąta A:
Z wierzchołka A zakreśl łuki o takim samym promieniu na bokach AC i AB. Punkty przecięcia oznacz literami P i Q.
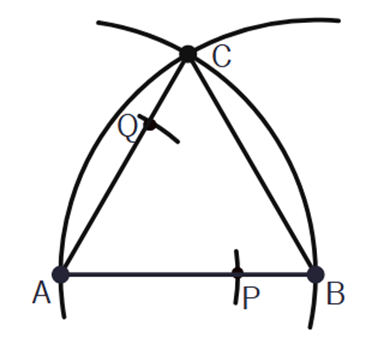
Z punktów P i Q zakreśl łuki o takim samym promieniu. Punkt ich przecięcia oznacz literą R.
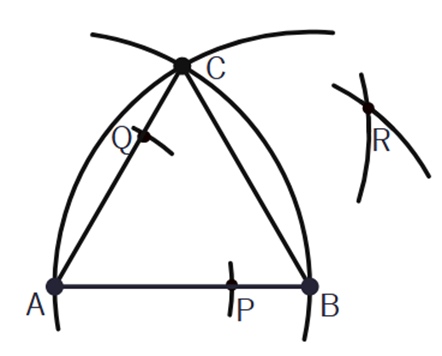
Narysuj półprostą wychodząca z wierzchołka A przecinająca punkt R. Jest to dwusieczna kąta A.
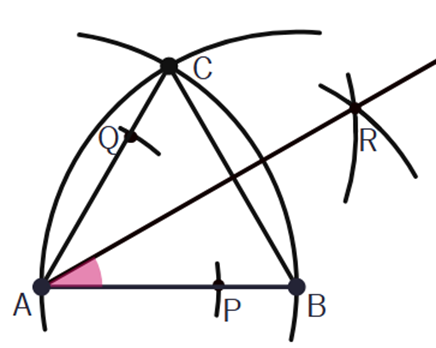
Zaznaczony kąt ma miarę
![]() .
.


Zadanie 1
272Zadanie 5
272Zadanie 6
272Zadanie 7
272Zadanie 8
272Zadanie 5
277Zadanie 6
277Zadanie 1
280Zadanie 2
281Zadanie 3
281Zadanie 4
281Zadanie 1
286Zadanie 2
287Zadanie 4
287Zadanie 5
287Zadanie 6
287Zadanie 7
287Zadanie 8
287Zadanie 9
287Zadanie 14
287Zadanie 2
291Zadanie 3
291Zadanie 4
291Zadanie 5
291Zadanie 1
298Zadanie 2
298Zadanie 5
298Zadanie 9
298Zadanie 10
298Zadanie 11
298Zadanie 1
302Zadanie 2
302Zadanie 9
303Zadanie 10
303Zadanie 11
303Zadanie 12
303Zadanie 1
309Zadanie 4
310Zadanie 5
310Zadanie 6
310Zadanie 7
310Zadanie 8
310Zadanie 9
310Zadanie 10
310Zadanie 11
310Zadanie 1
321Zadanie 2
321Zadanie 3
321Zadanie 4
322Zadanie 5
322Zadanie 6
322Zadanie 9
322Zadanie 10
329Zadanie 11
329Zadanie 15
329
