Udowodnij, że jeśli |EC| = 1, to kąt APB jest prosty, jeżeli w prostokącie ABCD boki mają długość: |AB| = 30, |BC| = 9, bok BC przedłużono poza punkt C do punktu E, a odcinek AE przecina bok DC w punkcie P.
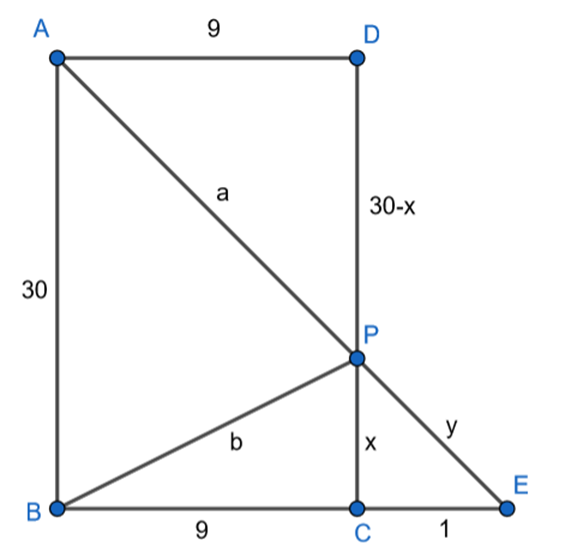
Proste AB i CD są równoległe.
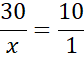
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Aby trójkąt APB był prostokątny:
![]()
![]()
![]()
![]()
Trójkąt jest prostokątny.

Wykonaj rysunek pomocniczy. Zauważ, że skoro proste AB i CD są równoległe to możesz skorzystać z twierdzenia Talesa w trójkątach ABE i PCE, aby wyznaczyć wartość
![]() .
.
Następnie skorzystaj z twierdzenia Pitagorasa w trójkątach BCP i ADP, aby wyznaczyć długości odcinków
![]() . Na koniec ustal, czy dla uzyskanych długości boków trójkąt jest prostokątny, czyli spełnione jest twierdzenie Pitagorasa.
. Na koniec ustal, czy dla uzyskanych długości boków trójkąt jest prostokątny, czyli spełnione jest twierdzenie Pitagorasa.

Zadanie 1
272Zadanie 5
272Zadanie 6
272Zadanie 7
272Zadanie 8
272Zadanie 5
277Zadanie 6
277Zadanie 1
280Zadanie 2
281Zadanie 3
281Zadanie 4
281Zadanie 1
286Zadanie 2
287Zadanie 4
287Zadanie 5
287Zadanie 6
287Zadanie 7
287Zadanie 8
287Zadanie 9
287Zadanie 14
287Zadanie 2
291Zadanie 3
291Zadanie 4
291Zadanie 5
291Zadanie 1
298Zadanie 2
298Zadanie 5
298Zadanie 9
298Zadanie 10
298Zadanie 11
298Zadanie 1
302Zadanie 2
302Zadanie 9
303Zadanie 10
303Zadanie 11
303Zadanie 12
303Zadanie 1
309Zadanie 4
310Zadanie 5
310Zadanie 6
310Zadanie 7
310Zadanie 8
310Zadanie 9
310Zadanie 10
310Zadanie 11
310Zadanie 1
321Zadanie 2
321Zadanie 3
321Zadanie 4
322Zadanie 5
322Zadanie 6
322Zadanie 9
322Zadanie 10
329Zadanie 11
329Zadanie 15
329
