Udowodnij, że trójkąt ALK jest prostokątny, jeśli boki prostokąta ABCD mają długość: |AB| = 4, |BC| = 6, K oznacza środek boku DC, zaś L – punkt leżący na boku BC i dzielący ten bok na dwa odcinki w stosunku 1 : 2.
1 przypadek:
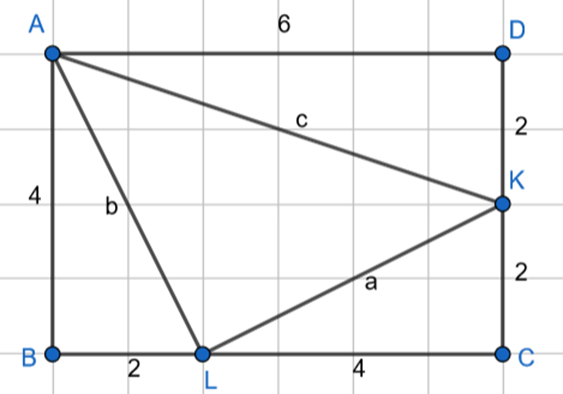
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Aby trójkąt był prostokątny:
![]()
![]()
![]()
![]()
Trójkąt jest prostokątny.
2 przypadek:
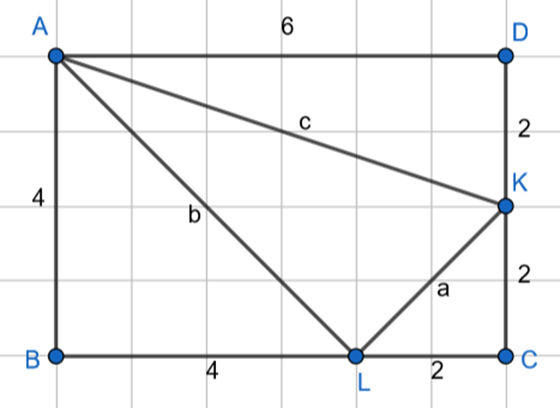
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Aby trójkąt był prostokątny:
![]()
![]()
![]()
![]()
Trójkąt jest prostokątny.

Wykonaj rysunek pomocniczy, a następnie skorzystaj z twierdzenia Pitagorasa w trójkątach ABL, KLC i ADK, aby wyznaczyć długości odcinków
![]() . Na koniec ustal, czy dla uzyskanych długości boków trójkąt jest prostokątny, czyli spełnione jest twierdzenie Pitagorasa.
. Na koniec ustal, czy dla uzyskanych długości boków trójkąt jest prostokątny, czyli spełnione jest twierdzenie Pitagorasa.
W podobny sposób wykaż, że w trójkąt w przypadku 2 jest prostokątny.

Zadanie 1
272Zadanie 5
272Zadanie 6
272Zadanie 7
272Zadanie 8
272Zadanie 5
277Zadanie 6
277Zadanie 1
280Zadanie 2
281Zadanie 3
281Zadanie 4
281Zadanie 1
286Zadanie 2
287Zadanie 4
287Zadanie 5
287Zadanie 6
287Zadanie 7
287Zadanie 8
287Zadanie 9
287Zadanie 14
287Zadanie 2
291Zadanie 3
291Zadanie 4
291Zadanie 5
291Zadanie 1
298Zadanie 2
298Zadanie 5
298Zadanie 9
298Zadanie 10
298Zadanie 11
298Zadanie 1
302Zadanie 2
302Zadanie 9
303Zadanie 10
303Zadanie 11
303Zadanie 12
303Zadanie 1
309Zadanie 4
310Zadanie 5
310Zadanie 6
310Zadanie 7
310Zadanie 8
310Zadanie 9
310Zadanie 10
310Zadanie 11
310Zadanie 1
321Zadanie 2
321Zadanie 3
321Zadanie 4
322Zadanie 5
322Zadanie 6
322Zadanie 9
322Zadanie 10
329Zadanie 11
329Zadanie 15
329
