Udowodnij, że ADE jest podobny do trójkąta EPD i oblicz skalę tego podobieństwa, jeśli w trójkącie równobocznym ABC poprowadzono środkowe AE i CD, które przecięły się w punkcie P.
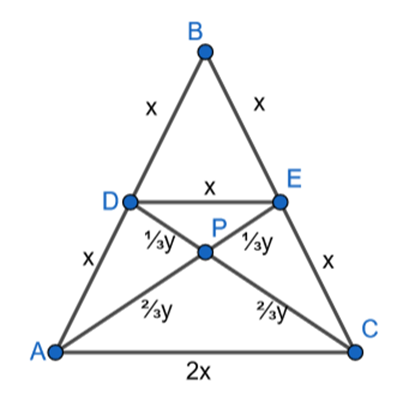
Jeśli w trójkącie połączymy środki dwóch boków, to powstały odcinek jest równoległy do boku trzeciego i jego długość jest równa połowie jego długości.
Oznacza to, że trójkąt ADE jest równoramienny, więc:
![]() oraz
oraz
![]()
Suma miar kątów w trójkącie wynosi
![]() , więc:
, więc:
![]()
Odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku, a środek ciężkości jest punktem przecięcia środkowych w trójkącie oraz dzieli on każdą ze środkowych w stosunku 2 : 1 licząc od wierzchołka.
Oznacza to, że trójkąt DPE jest równoramienny, więc:
![]() oraz
oraz
![]()
Suma miar kątów w trójkącie wynosi
![]() , więc:
, więc:
![]()
Trójkąty ADE i EPD są podobne z cechy KKK
![]() .
.
Środkowe trójkąta równobocznego są jednocześnie jego wysokościami, więc trójkąt ADC jest prostokątny:
![]()
![]()
![]()
![]()
![]()
Jeśli trójkąty są podobne to odpowiadające sobie długości boków (czyli znajdujące się pomiędzy tymi sami kątami) są tak samo proporcjonalne względem siebie i wartość ilorazu ich długości jest stale równa skali
![]() .
.
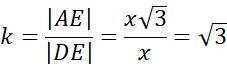


Zadanie 1
272Zadanie 5
272Zadanie 6
272Zadanie 7
272Zadanie 8
272Zadanie 5
277Zadanie 6
277Zadanie 1
280Zadanie 2
281Zadanie 3
281Zadanie 4
281Zadanie 1
286Zadanie 2
287Zadanie 4
287Zadanie 5
287Zadanie 6
287Zadanie 7
287Zadanie 8
287Zadanie 9
287Zadanie 14
287Zadanie 2
291Zadanie 3
291Zadanie 4
291Zadanie 5
291Zadanie 1
298Zadanie 2
298Zadanie 5
298Zadanie 9
298Zadanie 10
298Zadanie 11
298Zadanie 1
302Zadanie 2
302Zadanie 9
303Zadanie 10
303Zadanie 11
303Zadanie 12
303Zadanie 1
309Zadanie 4
310Zadanie 5
310Zadanie 6
310Zadanie 7
310Zadanie 8
310Zadanie 9
310Zadanie 10
310Zadanie 11
310Zadanie 1
321Zadanie 2
321Zadanie 3
321Zadanie 4
322Zadanie 5
322Zadanie 6
322Zadanie 9
322Zadanie 10
329Zadanie 11
329Zadanie 15
329
