Udowodnij, że
![]() , jeśli w trójkącie równoramiennym ABC, |AC| = |BC|, punkty K, L, M są odpowiednio środkami boków AC, AB, BC, prosta ML przecina się w punkcie P z prostą prostopadłą do odcinka KM i przechodzącą przez punkt K.
, jeśli w trójkącie równoramiennym ABC, |AC| = |BC|, punkty K, L, M są odpowiednio środkami boków AC, AB, BC, prosta ML przecina się w punkcie P z prostą prostopadłą do odcinka KM i przechodzącą przez punkt K.
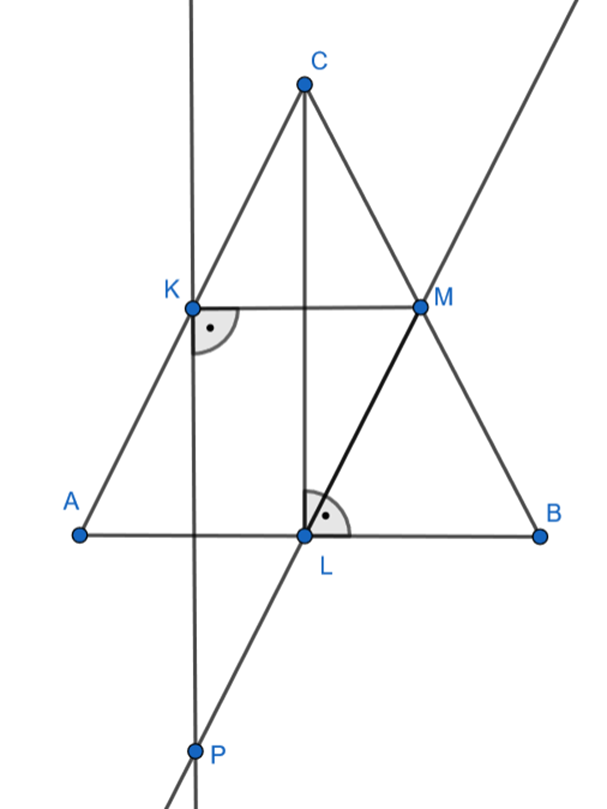
Twierdzenie: Jeśli w trójkącie połączymy środki dwóch boków, to powstały odcinek jest równoległy do boku trzeciego i jego długość jest równa połowie jego długości.
Oznacza to, że proste AK i ML, AL i KM są równoległe oraz
![]() i
i
![]() .
.
Więc czworokąt ALKM jest równoległobokiem, którego przeciwległe kąty mają takie same miary, więc:
![]() .
.
Oznacza to, że trójkąty ACL i KPM są przystające z cechy KBK
![]() .
.
Trójkąt ABC jest równoramienny, więc
![]() a wysokość dzieli podstawę na pół, czyli:
a wysokość dzieli podstawę na pół, czyli:
![]() .
.
Oznacza to, że trójkąty ACL i LBC są przystające z cechy KBK
![]() .
.
Skoro trójkąty ACL i KPM oraz ACL i LBC są przystające, to trójkąty KPM i LBC są również.
To kończy dowód.


Zadanie 1
272Zadanie 5
272Zadanie 6
272Zadanie 7
272Zadanie 8
272Zadanie 5
277Zadanie 6
277Zadanie 1
280Zadanie 2
281Zadanie 3
281Zadanie 4
281Zadanie 1
286Zadanie 2
287Zadanie 4
287Zadanie 5
287Zadanie 6
287Zadanie 7
287Zadanie 8
287Zadanie 9
287Zadanie 14
287Zadanie 2
291Zadanie 3
291Zadanie 4
291Zadanie 5
291Zadanie 1
298Zadanie 2
298Zadanie 5
298Zadanie 9
298Zadanie 10
298Zadanie 11
298Zadanie 1
302Zadanie 2
302Zadanie 9
303Zadanie 10
303Zadanie 11
303Zadanie 12
303Zadanie 1
309Zadanie 4
310Zadanie 5
310Zadanie 6
310Zadanie 7
310Zadanie 8
310Zadanie 9
310Zadanie 10
310Zadanie 11
310Zadanie 1
321Zadanie 2
321Zadanie 3
321Zadanie 4
322Zadanie 5
322Zadanie 6
322Zadanie 9
322Zadanie 10
329Zadanie 11
329Zadanie 15
329
