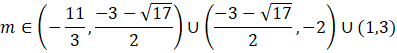![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
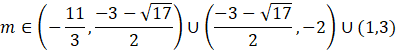
ODP: Warunki zapisane w treści zadania spełniają
![]() .
.

Oblicz miejsca zerowe każdego z nawiasów.
![]()
![]()
![]()
![]()
Oznacza to, że jednym z rozwiązań równania jest 4.
Zauważ, że aby równanie w drugim nawiasie miało dwa miejsca zerowe, to delta musi być większa od zera. Wyznacz ją.
![]()
![]()
Oblicz deltę z delty i jej miejsca zerowe.
![]()
![]()
![]()
![]()
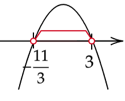
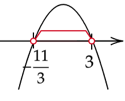
Obliczone miejsca zerowe zaznacz na osi. Ramiona paraboli skieruj w dół, ponieważ współczynnik stojący przy
![]() z najwyższą potęgą jest ujemny. Zaznacz przedział w którym parabola jest nad osią.
z najwyższą potęgą jest ujemny. Zaznacz przedział w którym parabola jest nad osią.
![]()
Zauważ, że aby równanie miało trzy różne rozwiązania, to miejscem zerowym drugiego nawiasu nie może być 4. Wyklucz
![]() dla których rozwiązaniem równania
dla których rozwiązaniem równania
![]() jest 4.
jest 4.
![]()
![]()
![]()
Oblicz deltę i miejsca zerowe.
![]()
![]()
![]()
![]()
![]()
Pozostało rozwiązać warunek zawarty w treści zadania. Zauważ, że jednym z miejsc zerowych jest 4. Wstaw ją w miejsce
![]() .
.
![]()
Przekształć nierówność do otrzymania postaci ze wzorami Viete’a.
![]()
![]()
![]()
Zastosuj wzory Viete’a do powyższej nierówności.
![]()
![]()
![]()
![]()
Oblicz deltę i miejsca zerowe.
![]()
![]()
![]()
![]()
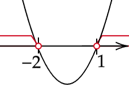
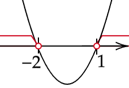
Obliczone miejsca zerowe zaznacz na osi. Ramiona paraboli skieruj w górę, ponieważ współczynnik stojący przy
![]() z najwyższą potęgą jest dodatni. Zaznacz przedział w którym parabola jest nad osią.
z najwyższą potęgą jest dodatni. Zaznacz przedział w którym parabola jest nad osią.
![]()
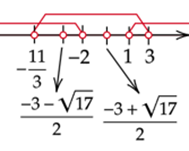
Zaznacz wszystkie przedziały i wykluczone
![]() na osi.
na osi.
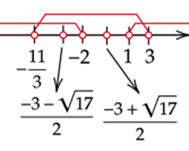
Rozwiązaniem zadania są
![]() spełniające wszystkie warunki. Zapisz je.
spełniające wszystkie warunki. Zapisz je.