Matura z matematyki. Arkusz dodatkowy. Poziom rozszerzony. Czerwiec 2022

Arkusz egzaminacyjny, Wydawnictwo: CKE

Zadanie 14 - strona 20

Wyznacz równanie okręgu o₂ o promieniu $\text{[math]}$ , jeśli dany jest okrąg o₁ o równaniu $\text{[math]}$ , ich środki leżą po różnych stronach prostej k o równaniu y = −3x − 6, a punkty wspólne obu okręgów leżą na prostej k.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

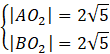
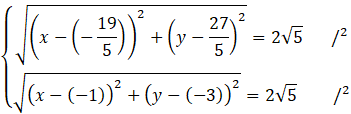
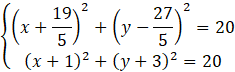
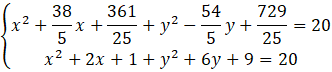
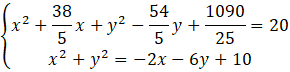
Środek okręgu $\text{[math]}$ nie spełnia warunków zadania.

$\text{[math]}$

$\text{[math]}$

ODP: Okrąg $\text{[math]}$ ma równanie $\text{[math]}$ .

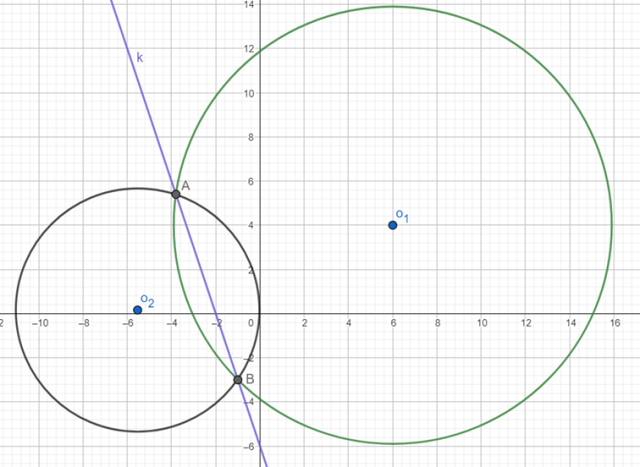
Wykonaj rysunek pomocniczy:

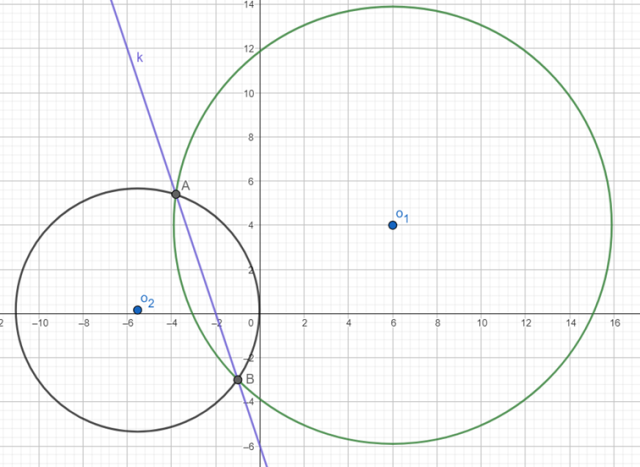
Oblicz współrzędne punktów przecięcia okręgu $\text{[math]}$ i prostej $\text{[math]}$ Zapisz je za pomocą układu równań.

$\text{[math]}$

Wartość $\text{[math]}$ z drugiego równania podstaw pod pierwsze.

$\text{[math]}$

Rozwiąż powstałe równanie. Oblicz deltę i miejsca zerowe.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Zapisz współrzędne punktów A i B.

$\text{[math]}$

Niech $\text{[math]}$ .

Skorzystaj ze wzoru na długość odcinka. Zauważ, że odcinki AO₂ i BO₂ są równe promieniowi tego okręgu.

$\text{[math]}$

$\text{[math]}$

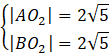
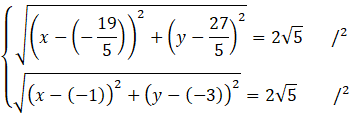
Powstałe równania zapisz w jak najprostszych postaciach.

$\text{[math]}$

$\text{[math]}$

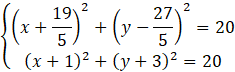
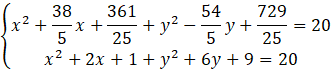
Z drugiego równania wyznacz wartość $\text{[math]}$ i podstaw ją w miejsce pierwszego równania.

$\text{[math]}$

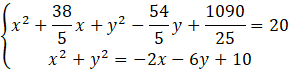
Powstałe równanie zapisz w jak najprostszej postaci i wyznacz z niego wartość $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Uzyskaną wartość $\text{[math]}$ podstaw pod dolne równanie z układu równań.

$\text{[math]}$

Rozwiąż powstałe równanie. Oblicz deltę i miejsca zerowe.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Zapisz możliwe środki okręgu.

$\text{[math]}$

Zauważ, że środek okręgu $\text{[math]}$ nie spełnia warunków zadania, ponieważ dla takich współrzędnych nie leżałby po drugiej stronie prostej $\text{[math]}$ w porównaniu do środka okręgu $\text{[math]}$

$\text{[math]}$

Zapisz równanie okręgu $\text{[math]}$ .

$\text{[math]}$

Zadanie 34., strona 217, Prosto do matury. Matematyka. Klasa 2. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 6, strona 107, MATeMAtyka 1. Karty pracy ucznia. Zakres podstawowy

Zadanie 11., strona 158, Matematyka wokół nas. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 6, strona 22, Matematyka. Klasa 7. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 15., strona 14, Matematyka z plusem. Klasa 6. Zeszyt ćwiczeń. Wersja A. Część 1 – rozwiązania i odpowiedzi

Ćwiczenie 15., strona 77, Matematyka z Plusem. Liczby naturalne i ułamki zwykłe. Klasa 5. Zeszyt ćwiczeń. Wersja A. Część 1/3 - rozwiązania i odpowiedzi

Zadanie 112, strona 139, Matematyka. Klasa 2. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 8, strona 63, Matematyka wokół nas. Klasa 7. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 12., strona 347, Matematyka. Klasa 4. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 16, strona 99, Matematyka z plusem. Klasa 6. Zbiór zadań – rozwiązania i odpowiedzi

2

2

2

2

4

5

6

8

10

12

14

16

18

20

Zadanie 15

22

22

22

22

Pełny spis treści