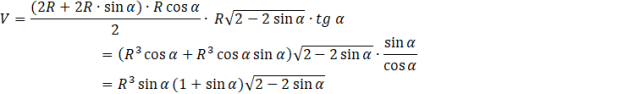![]() - wysokość trapezu opuszczona z wierzchołka D
- wysokość trapezu opuszczona z wierzchołka D
![]() – wysokość graniastosłupa
– wysokość graniastosłupa
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
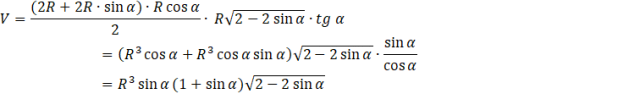
ODP: Objętość graniastosłupa w zależności od promienia
![]() i kąta
i kąta
![]() wynosi
wynosi
![]() .
.

Oznacz jako:
![]() - wysokość trapezu opuszczona z wierzchołka D opadająca w punkcie E
- wysokość trapezu opuszczona z wierzchołka D opadająca w punkcie E
![]() – wysokość graniastosłupa
– wysokość graniastosłupa
Zauważ, że kąt CAD jest kątem wpisanym opartym na tym samym łuku co kąt środkowy DOC, więc jego miara jest od niego dwukrotnie mniejsza.
![]()
Zauważ, że okrąg opisany na trapezie ABCD jest również okręgiem opisanym na trójkącie ACD. Skorzystaj z twierdzenia sinusów w tym trójkącie i oblicz długość odcinka CD.
![]()
![]()
Trójkąty AOD, DOC i BOC tworzą kąt półpełny, przy czym kąty AOD i BOC są równe. Na tej podstawie oblicz ich miarę.
![]()
Skorzystaj z własności funkcji trygonometrycznych w trójkącie EDO i oblicz wartość wysokości trójkąta i jednocześnie trapezu.
![]()
![]()
Skorzystaj z własności funkcji trygonometrycznych w trójkącie
![]() oraz tego, że przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze
oraz tego, że przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze
![]() i oblicz wysokość graniastosłupa.
i oblicz wysokość graniastosłupa.
![]()
![]()
Zastosuj twierdzenie cosinusów w trójkącie AOD i oblicz miarę ramienia trapezu AD.
![]()
![]()
Podstaw obliczoną długość odcinka AD pod wartość wysokości
![]() .
.
![]()
Zapisz wzór na objętość ostrosłupa o podstawie trapezu ABCD.
![]()
Podstaw obliczone wartości i doprowadź równanie do najprostszej postaci.