Oblicz długość odcinka $\text{[math]}$ , dla którego pole wyrażone wzorem $\text{[math]}$ jest największe.

$\text{[math]}$

ODP: Funkcja $\text{[math]}$ ma największe pole dla $\text{[math]}$ .

$\text{[math]}$

Zauważ, że wartość znajdująca się pod pierwiastkiem musi być dodatnia. Oblicz dla jakich $\text{[math]}$ jest to spełnione. Pamiętaj, że $\text{[math]}$ , bo długość odcinka musi być dodatnia.

$\text{[math]}$

Zapisz wspólny przedział trzech powyższych nierówności.

$\text{[math]}$

Zapisz równanie funkcji $\text{[math]}$ w postaci wyrażenia pod jednym pierwiastkiem.

$\text{[math]}$

Zapisz funkcję pomocniczą zmiennej $\text{[math]}$ . Skorzystaj z wartości pod pierwiastkiem.

$\text{[math]}$

Oblicz pochodną funkcji.

$\text{[math]}$

Sprawdź, czy liczba -1 jest miejscem zerowym pochodnej funkcji.

$\text{[math]}$ - tak

Dokonaj dzielenia pochodnej przez dwumian $\text{[math]}$ , aby obliczyć jej pozostałe miejsca zerowe.

$\text{[math]}$

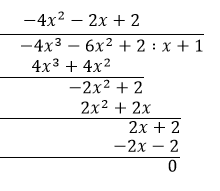
Oblicz deltę i miejsca zerowe równania z drugiego nawiasu.

$\text{[math]}$

Zaznacz uzyskane miejsca zerowe na osi

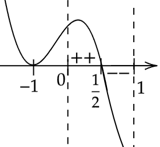
Oznacza to, że pochodna w przedziale $\text{[math]}$ ma jedno miejsce zerowe $\text{[math]}$ i zmienia w tym punkcie znak z dodatniego na ujemny. W takim razie funkcja $\text{[math]}$ (oraz $\text{[math]}$ ) rośnie w przedziale $\text{[math]}$ ,a maleje w przedziale $\text{[math]}$ . Więc będzie do największa wartość pochodnej: