Oblicz brakujące współrzędne trójkąta ABC. Którego okrąg wpisany ma równanie
, a współrzędne punktu A wynoszą (7,-1).
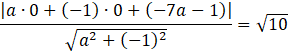
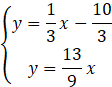
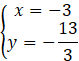
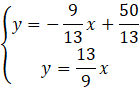
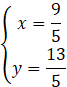
ODP.:
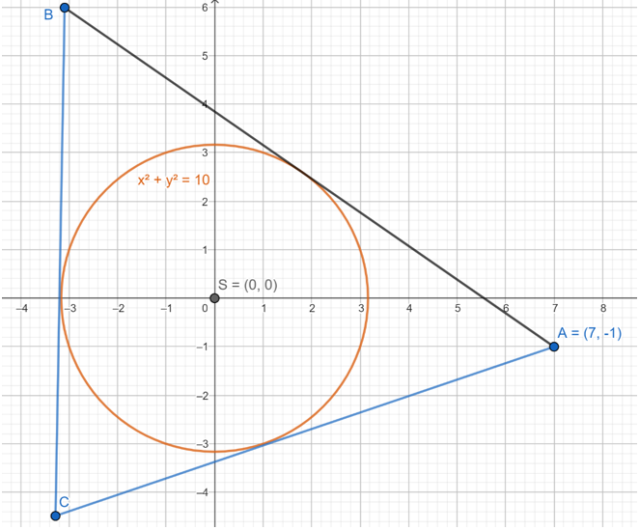
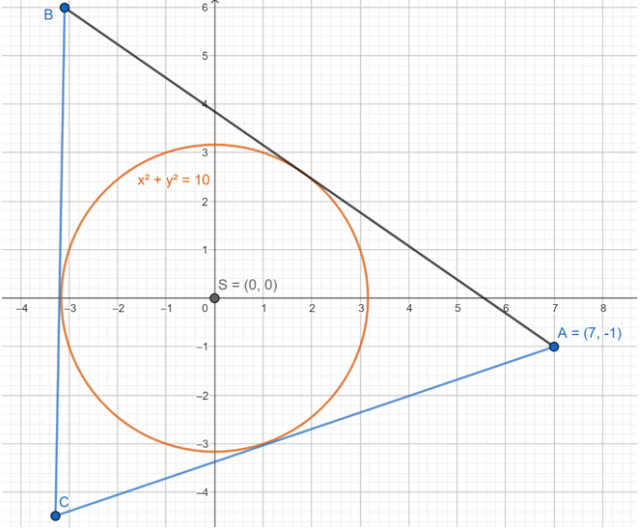
Wykonaj rysunek pomocniczy.
Skorzystaj ze wzoru na równanie kierunkowe prostej o współczynniku kierunkowym a, która przechodzi przez punkt
W ten sposób znajdziesz równania prostych AC i AB przechodzących przez punkt A.
Przedstaw równanie funkcji w postaci ogólnej.
Zauważ, że obie proste są styczne do okręgu, więc ich odległość od środka okręgu wynosi
Skorzystaj ze wzoru na odległość punktu S od prostej.
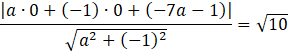
Przenieś wszystko na lewą stronę.
Zauważ, że powstało równanie kwadratowe. Oblicz deltę i miejsca zerowe.
Podstaw wyliczone wartości a pod równanie prostej
.
Zauważ, że pierwsza prosta jest rosnąca (a>0), a druga malejąca (a<0).
Prosta CS jest prostopadła do prostej AB. Oznacza to, że jej współczynnik kierunkowy jest przeciwny i odwrotny do prostej AB.
Prosta CS przechodzi przez punkt S. Podstaw jest współrzędne i oblicz wartość współczynnika b.
Zauważ, że punkt C jest miejscem przecięcia prostych CS i AC.
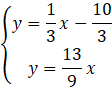
Skorzystaj z metody podstawienia i podstaw wartość z drugiego równania pod pierwsze.
Z powstałego równania wylicz wartość x.
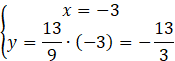
Oblicz współrzędne środka odcinka AB. Będzie to punkt przecięcia prostych AB i CS.
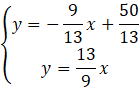
Skorzystaj z metody podstawienia i podstaw wartość z drugiego równania pod pierwsze.
Z powstałego równania wylicz wartość x.
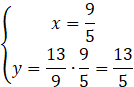
Skorzystaj ze wzoru na środek odcinka AB, aby obliczyć współrzędne punktu B.
