Skonstruuj trójkąt z trzech wybranych odcinków. Czy wybrane odcinki muszą spełniać jakiś warunek?
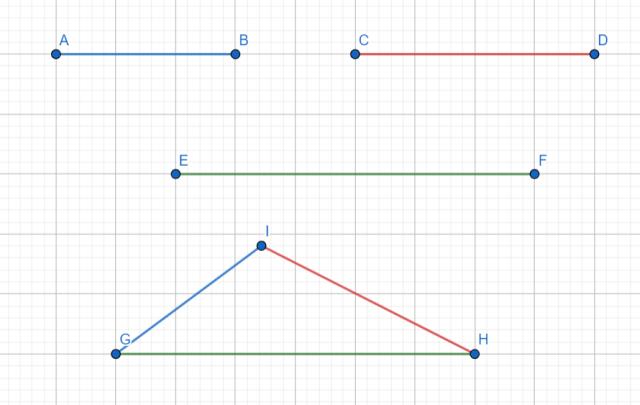
Odcinki muszą spełniać warunek trójkąta, tzn. |AB|+|CD| > |EF|

Narysuj odcinki AB, CD i EF, a następnie wykonaj następujące kroki:
· przerysuj odcinek EF poniżej i oznacz go jako GH;
· z punktu G wykonaj łuk cyrklem długości odcinka AB;
· z punktu H wykonaj łuk cyrklem długości odcinka CD;
· punkt przecięcia obu łuków (punkt I) będzie trzecim wierzchołkiem trójkąta.
Aby z trzech odcinków można było zbudować trójkąt, to muszą one spełniać warunek trójkąta, czyli suma dwóch krótszych boków musi być dłuższa od trzeciego boku.

Zadanie 1.1.
214Zadanie 1.4.
215Zadanie 1.8.
215Zadanie 1.13.
215Zadanie 1.18.
216Zadanie 1.19.
216Zadanie 1.24.
216Zadanie 1.27.
216Zadanie 2.4.
227Zadanie 2.5.
227Zadanie 2.9.
228Zadanie 2.14.
229Zadanie 3.6.
244Zadanie 3.15.
244Zadanie 3.17.
245Zadanie 3.18.
245Zadanie 4.6.
252Zadanie 4.7.
252Zadanie 4.8.
253Zadanie 4.9.
253Zadanie 4.10.
253Zadanie 4.11.
253Zadanie 4.12.
253Zadanie 4.15.
253Zadanie 2.
254Zadanie 4.
254Zadanie 5.5.
260Zadanie 5.7.
260Zadanie 5.8.
261Zadanie 2.
262Zadanie 6.4.
269Zadanie 6.5.
270Zadanie 6.6.
270Zadanie 6.8.
270Zadanie 3
272Zadanie 7.5.
278Zadanie 7.7.
279Zadanie 7.9.
279Zadanie 7.10.
279Zadanie 7.12.
279Zadanie 8.5.
296Zadanie 8.6.
296Zadanie 8.7.
296Zadanie 8.13.
297
