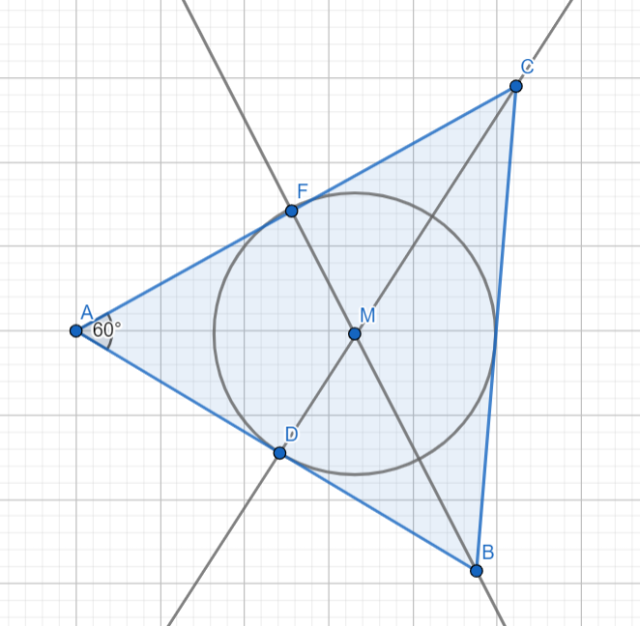
W trójkącie ABC poprowadzono dwusieczne CD i BF, które przecinają się w punkcie M. Wykaż, że jeżeli kąt przy wierzchołku A ma miarę 60°, to na czworokącie ADMF można opisać okrąg.
Dwusieczne kątów trójkąta przecinają się w jednym punkcie – w trójkąt można wpisać okrąg.
Z tw. o odcinkach stycznych:
![]()
Trójkąt AFD – równoboczny
![]()
![]()
![]()
Trójkąt MFD – równoramienny
![]()
![]()
Na czworokącie można opisać okrąg.

Zauważ, że w trójkąt ABC można wpisać okrąg, a więc można skorzystać z twierdzenia o odcinkach stycznych. Trójkąt AFD jest trójkątem równobocznym, a trójkąt MFD – równoramiennym. Oblicz miary ich kątów i zauważ, że kąt DMF ma 120°. Suma naprzemianległych kątów czworokąta ADMF jest równa, więc można opisać na nim okrąg.

Zadanie 1.1.
214Zadanie 1.4.
215Zadanie 1.8.
215Zadanie 1.13.
215Zadanie 1.18.
216Zadanie 1.19.
216Zadanie 1.24.
216Zadanie 1.27.
216Zadanie 2.4.
227Zadanie 2.5.
227Zadanie 2.9.
228Zadanie 2.14.
229Zadanie 3.6.
244Zadanie 3.15.
244Zadanie 3.17.
245Zadanie 3.18.
245Zadanie 4.6.
252Zadanie 4.7.
252Zadanie 4.8.
253Zadanie 4.9.
253Zadanie 4.10.
253Zadanie 4.11.
253Zadanie 4.12.
253Zadanie 4.15.
253Zadanie 2.
254Zadanie 4.
254Zadanie 5.5.
260Zadanie 5.7.
260Zadanie 5.8.
261Zadanie 2.
262Zadanie 6.4.
269Zadanie 6.5.
270Zadanie 6.6.
270Zadanie 6.8.
270Zadanie 3
272Zadanie 7.5.
278Zadanie 7.7.
279Zadanie 7.9.
279Zadanie 7.10.
279Zadanie 7.12.
279Zadanie 8.5.
296Zadanie 8.6.
296Zadanie 8.7.
296Zadanie 8.13.
297
