W czworokąt ABCD wpisano okrąg. Środek tego okręgu jest punktem przecięcia przekątnych równoległoboku. Wykaż, że czworokąt ABCD jest rombem.
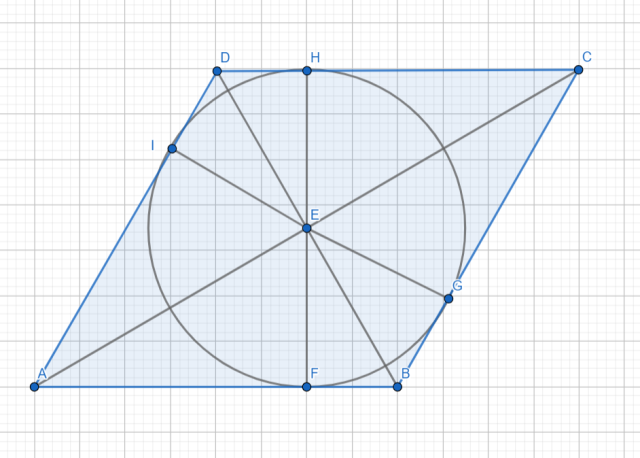
Styczne przechodzą pod kątem prostym:
![]()
EFBG, EHDI – deltoidy przystające
HF i IG – wysokości, więc
ABCD – równoległobok
![]()
![]()
![]()
ABCD – romb

Zauważ, że figury EFBG i EHDI są deltoidami przystającymi o dwóch kątach prostych. Odcinki HF i IG są wysokościami, więc czworokąt ABCD musi być równoległobokiem. Trójkąty ADB i CDB są przystające z cechy kąt – bok – kąt, więc wszystkie boki równoległoboku są równe. Z tego wynika, że ten równoległobok jest rombem.

Zadanie 1.1.
214Zadanie 1.4.
215Zadanie 1.8.
215Zadanie 1.13.
215Zadanie 1.18.
216Zadanie 1.19.
216Zadanie 1.24.
216Zadanie 1.27.
216Zadanie 2.4.
227Zadanie 2.5.
227Zadanie 2.9.
228Zadanie 2.14.
229Zadanie 3.6.
244Zadanie 3.15.
244Zadanie 3.17.
245Zadanie 3.18.
245Zadanie 4.6.
252Zadanie 4.7.
252Zadanie 4.8.
253Zadanie 4.9.
253Zadanie 4.10.
253Zadanie 4.11.
253Zadanie 4.12.
253Zadanie 4.15.
253Zadanie 2.
254Zadanie 4.
254Zadanie 5.5.
260Zadanie 5.7.
260Zadanie 5.8.
261Zadanie 2.
262Zadanie 6.4.
269Zadanie 6.5.
270Zadanie 6.6.
270Zadanie 6.8.
270Zadanie 3
272Zadanie 7.5.
278Zadanie 7.7.
279Zadanie 7.9.
279Zadanie 7.10.
279Zadanie 7.12.
279Zadanie 8.5.
296Zadanie 8.6.
296Zadanie 8.7.
296Zadanie 8.13.
297
