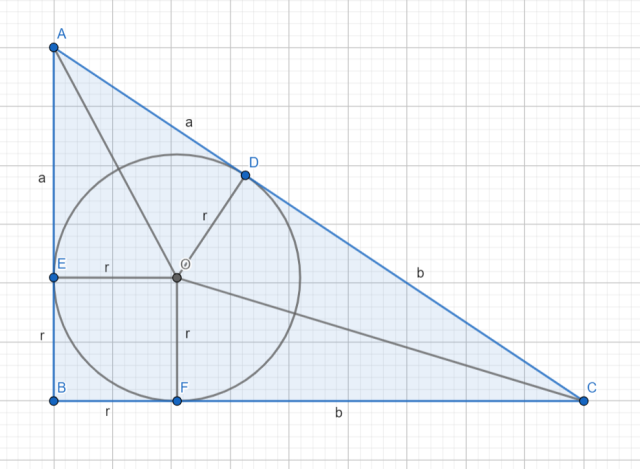
W trójkąt prostokątny wpisano okrąg. Punkt styczności dzieli przyprostokątną na dwa odcinki długości a i b. Udowodnij, że pole tego trójkąta można zapisać jako ab.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Skorzystaj z twierdzenia o odcinkach stycznych i zapisz długości przyprostokątnych jako a + r i b + r, gdzie r to długość promienia okręgu. Policz pole na dwa sposoby: najpierw jako połowa iloczynu przyprostokątnych, a następnie jako suma pól czterech trójkątów prostokątnych i kwadratu. Porównaj ze sobą oba wyniki i zauważ, że czynnik ab można przedstawić jako jeden ze sposobów zapisu pola trójkąta.

Zadanie 1.1.
214Zadanie 1.4.
215Zadanie 1.8.
215Zadanie 1.13.
215Zadanie 1.18.
216Zadanie 1.19.
216Zadanie 1.24.
216Zadanie 1.27.
216Zadanie 2.4.
227Zadanie 2.5.
227Zadanie 2.9.
228Zadanie 2.14.
229Zadanie 3.6.
244Zadanie 3.15.
244Zadanie 3.17.
245Zadanie 3.18.
245Zadanie 4.6.
252Zadanie 4.7.
252Zadanie 4.8.
253Zadanie 4.9.
253Zadanie 4.10.
253Zadanie 4.11.
253Zadanie 4.12.
253Zadanie 4.15.
253Zadanie 2.
254Zadanie 4.
254Zadanie 5.5.
260Zadanie 5.7.
260Zadanie 5.8.
261Zadanie 2.
262Zadanie 6.4.
269Zadanie 6.5.
270Zadanie 6.6.
270Zadanie 6.8.
270Zadanie 3
272Zadanie 7.5.
278Zadanie 7.7.
279Zadanie 7.9.
279Zadanie 7.10.
279Zadanie 7.12.
279Zadanie 8.5.
296Zadanie 8.6.
296Zadanie 8.7.
296Zadanie 8.13.
297
