Na okręgu o środku S zaznaczono punkty A, B i C tak, że odcinek AC jest średnicą, odcinek AB – cięciwą, a kąt między nimi ma miarę 20°. Oblicz miary wszystkich kątów w trójkątach ABC i ABS.
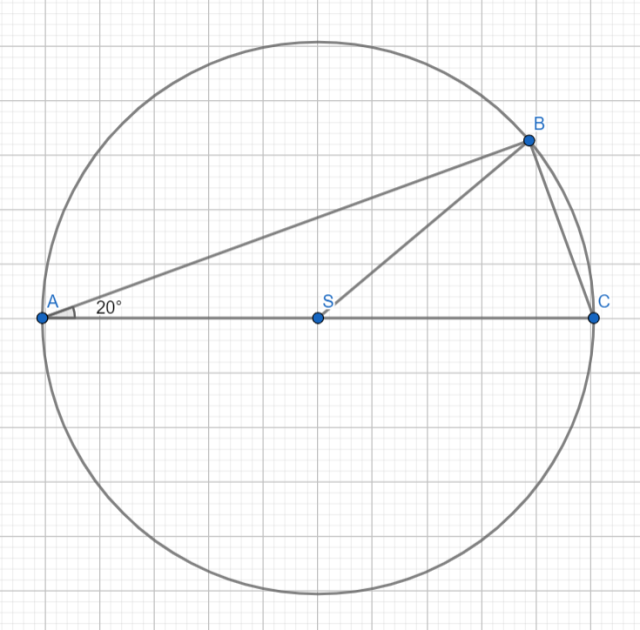
Trójkąt ABS – równoramienny
![]()
![]()
Trójkąt ABC – prostokątny (oparty na średnicy okręgu)
![]()
![]()

Zauważ, że trójkąt ABS jest równoramienny, bo dwa z jego boków są promieniami okręgu. Trójkąt ABC jest trójkątem prostokątnym, bo jeden z jego boków jest średnicą okręgu. Powyliczaj wszystkie boki, korzystając z sumy kątów w trójkącie.

Zadanie 1.1.
214Zadanie 1.4.
215Zadanie 1.8.
215Zadanie 1.13.
215Zadanie 1.18.
216Zadanie 1.19.
216Zadanie 1.24.
216Zadanie 1.27.
216Zadanie 2.4.
227Zadanie 2.5.
227Zadanie 2.9.
228Zadanie 2.14.
229Zadanie 3.6.
244Zadanie 3.15.
244Zadanie 3.17.
245Zadanie 3.18.
245Zadanie 4.6.
252Zadanie 4.7.
252Zadanie 4.8.
253Zadanie 4.9.
253Zadanie 4.10.
253Zadanie 4.11.
253Zadanie 4.12.
253Zadanie 4.15.
253Zadanie 2.
254Zadanie 4.
254Zadanie 5.5.
260Zadanie 5.7.
260Zadanie 5.8.
261Zadanie 2.
262Zadanie 6.4.
269Zadanie 6.5.
270Zadanie 6.6.
270Zadanie 6.8.
270Zadanie 3
272Zadanie 7.5.
278Zadanie 7.7.
279Zadanie 7.9.
279Zadanie 7.10.
279Zadanie 7.12.
279Zadanie 8.5.
296Zadanie 8.6.
296Zadanie 8.7.
296Zadanie 8.13.
297
