Na okręgu o środku S zaznaczono punkty A i B. Przez punkt B przechodzi styczna do okręgu, która przecina się z prostą AS w punkcie C pod kątem ![]()
1.
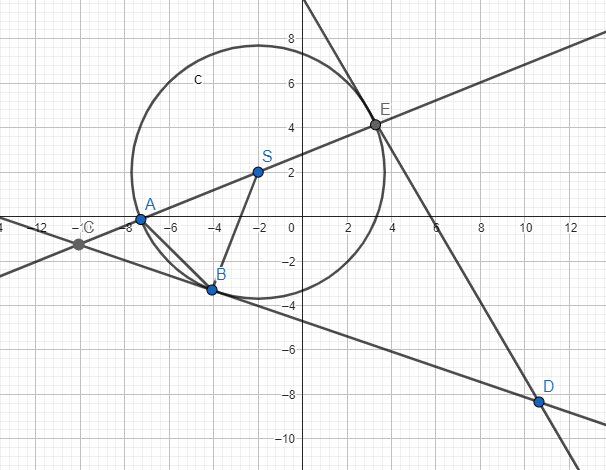
Z trójkąta SBC: ![]()
![]()
![]()
![]()
![]()
2.
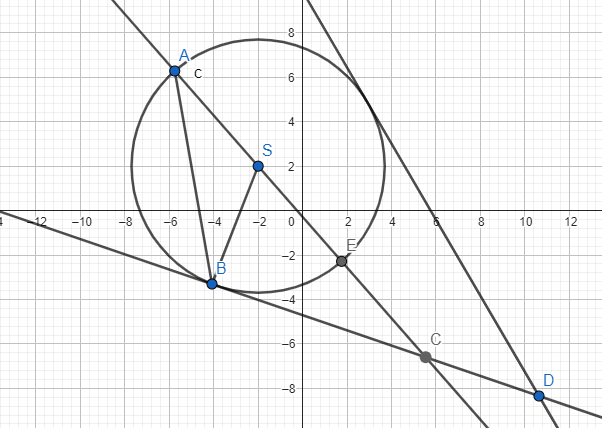
Z trójkąta SBC: ![]()
Zauważmy, że ![]()
![]()
![]()
![]()

Rozważ dwa przypadki: gdy punkt C leży na odcinku BD i gdy leży poza tym odcinkiem. W pierwszym przypadku skorzystaj z faktu, że kąt SBC jest prosty i wylicz miarę kąta CSB z sumy kątów w trójkącie oraz miarę kąta BSE korzystając z sumy kątów przyległych. Na koniec skorzystaj z twierdzenia o miarach kątów wpisanego i środkowego aby wyliczyć miarę kąta CAB. W drugim przypadku również zacznij od wyliczenia miary kąta CSB. Zauważ, że trójkąt SBE jest trójkątem równoramiennym i ponownie skorzystaj z twierdzenia o kącie wpisanym i środkowym aby obliczyć miarę szukanego kąta.

Zadanie 1.1.
214Zadanie 1.4.
215Zadanie 1.8.
215Zadanie 1.13.
215Zadanie 1.18.
216Zadanie 1.19.
216Zadanie 1.24.
216Zadanie 1.27.
216Zadanie 2.4.
227Zadanie 2.5.
227Zadanie 2.9.
228Zadanie 2.14.
229Zadanie 3.6.
244Zadanie 3.15.
244Zadanie 3.17.
245Zadanie 3.18.
245Zadanie 4.6.
252Zadanie 4.7.
252Zadanie 4.8.
253Zadanie 4.9.
253Zadanie 4.10.
253Zadanie 4.11.
253Zadanie 4.12.
253Zadanie 4.15.
253Zadanie 2.
254Zadanie 4.
254Zadanie 5.5.
260Zadanie 5.7.
260Zadanie 5.8.
261Zadanie 2.
262Zadanie 6.4.
269Zadanie 6.5.
270Zadanie 6.6.
270Zadanie 6.8.
270Zadanie 3
272Zadanie 7.5.
278Zadanie 7.7.
279Zadanie 7.9.
279Zadanie 7.10.
279Zadanie 7.12.
279Zadanie 8.5.
296Zadanie 8.6.
296Zadanie 8.7.
296Zadanie 8.13.
297
