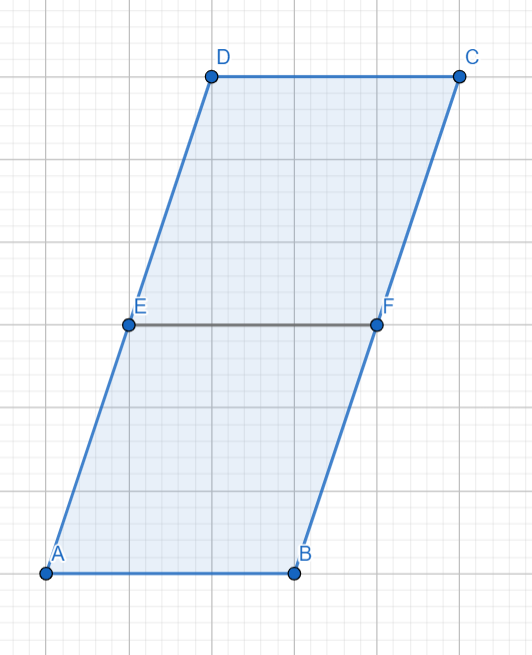
Boki BC i AD czworokąta ABCD są równe, a punkty E i F dzielą każdy z nich na pół. Udowodnij, że czworokąt ABCD jest równoległobokiem, jeżeli w czworokąty ABCD i FECD można wpisać okręgi.
Z warunku na okrąg wpisany w czworokąt:
![]()
![]()
Dodatkowo
![]()
![]()
Czyli
![]()
![]()
![]()
Czworokąt ABCD jest równoległobokiem.

Skorzystaj z warunku na okrąg wpisany w czworokąt, czyli że suma naprzeciwległych boków czworokąta musi być równa. Wiadomo, że punkty E i F dzielą boki czworokąta na pół. Rozpisz zależności między odpowiednimi odcinkami i zauważ, że odcinki AB i CD muszą być równe. Czworokąt, który posiada dwie pary boków równej długości jest równoległobokiem.

Zadanie 1.1.
214Zadanie 1.4.
215Zadanie 1.8.
215Zadanie 1.13.
215Zadanie 1.18.
216Zadanie 1.19.
216Zadanie 1.24.
216Zadanie 1.27.
216Zadanie 2.4.
227Zadanie 2.5.
227Zadanie 2.9.
228Zadanie 2.14.
229Zadanie 3.6.
244Zadanie 3.15.
244Zadanie 3.17.
245Zadanie 3.18.
245Zadanie 4.6.
252Zadanie 4.7.
252Zadanie 4.8.
253Zadanie 4.9.
253Zadanie 4.10.
253Zadanie 4.11.
253Zadanie 4.12.
253Zadanie 4.15.
253Zadanie 2.
254Zadanie 4.
254Zadanie 5.5.
260Zadanie 5.7.
260Zadanie 5.8.
261Zadanie 2.
262Zadanie 6.4.
269Zadanie 6.5.
270Zadanie 6.6.
270Zadanie 6.8.
270Zadanie 3
272Zadanie 7.5.
278Zadanie 7.7.
279Zadanie 7.9.
279Zadanie 7.10.
279Zadanie 7.12.
279Zadanie 8.5.
296Zadanie 8.6.
296Zadanie 8.7.
296Zadanie 8.13.
297
