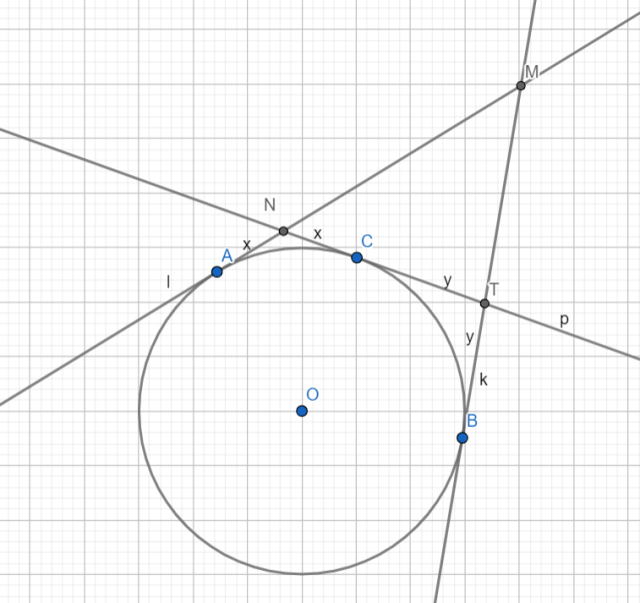
Na okręgu zaznaczono punkty A i B oraz punkt C na krótszym z wyznaczonych łuków. Przez wszystkie 3 punkty poprowadzono styczne do okręgu: styczną l w punkcie A, styczną k w punkcie B i styczną p w punkcie C. Punkt wspólny prostych l i k nazwano M, punkt wspólny prostych l i p – N, a prostych k i p – T. Oblicz długość odcinka MA, jeżeli obwód trójkąta jest równy 2a.
Tw. o odcinkach stycznych:
![]()
![]()
![]()
Obwód trójkąta MNT = 2a
![]()
![]()
![]()
![]()
![]()

Wykonaj rysunek poglądowy zgodny z treścią zadania. Skorzystaj z twierdzenia o odcinkach stycznych i wypisz pary odcinków równych. Zauważ, że podany obwód trójkąta jest równy sumie MA + MB. Jako że i te odcinki są sobie równe, długość odcinka MA jest równa połowie obwodu trójkąta, czyli a.

Zadanie 1.1.
214Zadanie 1.4.
215Zadanie 1.8.
215Zadanie 1.13.
215Zadanie 1.18.
216Zadanie 1.19.
216Zadanie 1.24.
216Zadanie 1.27.
216Zadanie 2.4.
227Zadanie 2.5.
227Zadanie 2.9.
228Zadanie 2.14.
229Zadanie 3.6.
244Zadanie 3.15.
244Zadanie 3.17.
245Zadanie 3.18.
245Zadanie 4.6.
252Zadanie 4.7.
252Zadanie 4.8.
253Zadanie 4.9.
253Zadanie 4.10.
253Zadanie 4.11.
253Zadanie 4.12.
253Zadanie 4.15.
253Zadanie 2.
254Zadanie 4.
254Zadanie 5.5.
260Zadanie 5.7.
260Zadanie 5.8.
261Zadanie 2.
262Zadanie 6.4.
269Zadanie 6.5.
270Zadanie 6.6.
270Zadanie 6.8.
270Zadanie 3
272Zadanie 7.5.
278Zadanie 7.7.
279Zadanie 7.9.
279Zadanie 7.10.
279Zadanie 7.12.
279Zadanie 8.5.
296Zadanie 8.6.
296Zadanie 8.7.
296Zadanie 8.13.
297
