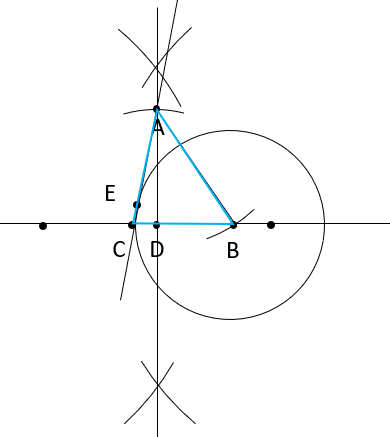
W tym zadaniu wykonać konstrukcję podanej figury.
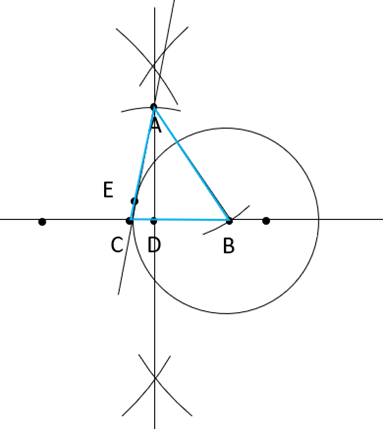

Skonstruuj dwie proste prostopadłe.
Wykreśl dowolną prostą i zaznacz na niej odcinek.

Wbij cyrkiel w jeden z końców odcinka i zakreśl łuki nad i pod odcinkiem mniej więcej na wysokości jego połowy.
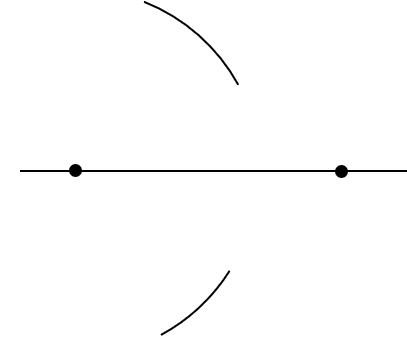
Powtórz to samo dla drugiego końca odcinka – nie zmieniaj rozwartości cyrkla!
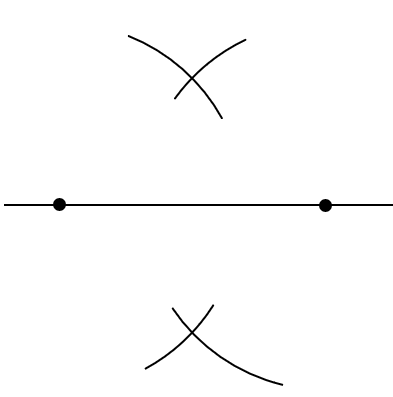
Połącz punkty przecięcia łuków. Punkt przecięcia prostych oznacz przez D.
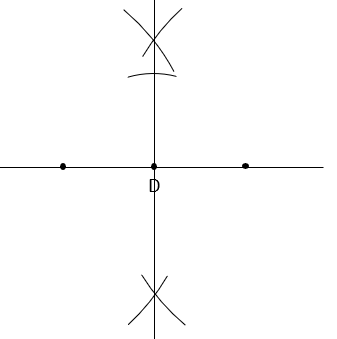
Odmierz cyrklem długość odcinka AD i odłóż go na jednej z prostych tak, by koniec odcinka znajdował się w punkcie przecięcia prostych. Koniec odcinka oznacz przez A.
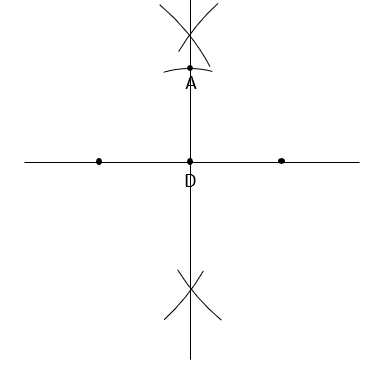
Odmierz długość odcinka AB. Wbij cyrkiel w punkt A i zakreśl łuk przecinający drugą z prostych prostopadłych. Otrzymany punkt oznacz przez B.
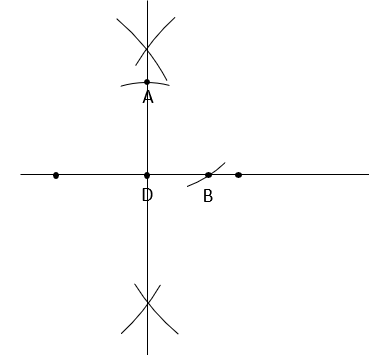
Odmierz długość odcinka BE. Wbij cyrkiel w punkt B i zakreśl okrąg o wyznaczonym promieniu.
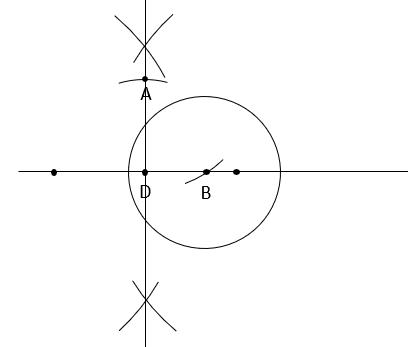
Skonstruuj styczną do okręgu przechodzącą przez punkt A. Punkt wspólny stycznej i okręgu nazwij E.
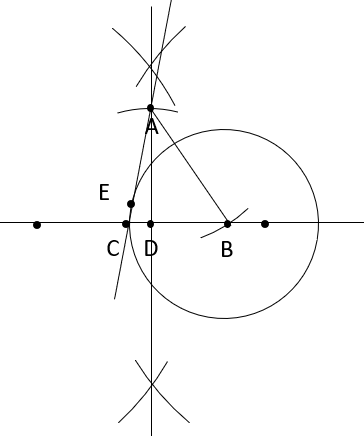
Punkt przecięcia stycznej z prostą DB wyznacza punkt C, będący trzecim wierzchołkiem trójkąta.

Ćwiczenie 1
177Ćwiczenie 2
178Ćwiczenie 14
182Zadanie 2
187Zadanie 3
187Zadanie 7
187Ćwiczenie 6
192Zadanie 2
193Zadanie 5
193Ćwiczenie 1
197Zadanie 1
199Zadanie 9
200Zadanie 11
200Zadanie 1
208Zadanie 2
208Zadanie 3
208Zadanie 4
208Zadanie 6
209Zadanie 3
221Zadanie 4
221Zadanie 5
221Zadanie 7
221Zadanie 8
221Zadanie 9
222Ćwiczenie 4
226Zadanie 3
227Zadanie 4
227Zadanie 9
227Zadanie 10
227Zadanie 12
227Ćwiczenie 2
228Ćwiczenie 4
231Zadanie 6
234Zadanie 7
234Zadanie 9
235Zadanie 11
235Zadanie 12
235Zadanie 17
235Zadanie 13
237Zadanie 18
238Zadanie 20
238Zadanie 26
238Zadanie 27
238Zadanie 31
239Zadanie 33
239Zadanie 36
239Zadanie 38
239
