W tym zadaniu musisz na dwa sposoby obliczyć promień okręgu wpisanego w trójkąt.
![]()
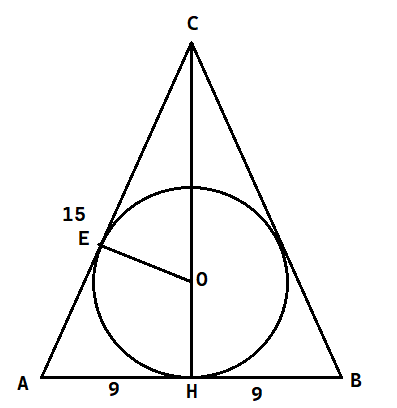
Sposób I:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Sposób II:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Na początku sprawdź, czy trójkąt jest ostrokątny, czy rozwartokątny. Aby to zrobić, oceń, czy suma kwadratów długości ramion jest większa (trójkąt ostrokątny), czy mniejsza (trójką rozwartokątny) od kwadratu długości podstawy.
Sposób I:
Korzystając z twierdzenia Pitagorasa dla trójkąta AHC oblicz wysokość trójkąta ABC. Następnie zauważ, że trójkąty CHA i CEO są trójkątami prostokątnymi o wspólnym kącie ostrym, a więc są one podobne na mocy cechy kąt – kąt – kąt. Porównaj ze sobą stosunki długości odpowiednich boków, otrzymując w ten sposób równanie, z którego wyznacz promień okręgu wpisanego w trójkąt ABC.
Sposób II:
Tak samo, jak w pierwszym sposobie oblicz wysokość trójkąta. Następnie zauważ, że na mocy twierdzenia o odcinkach stycznych, odcinki AE i AH mają równe długości. Długość odcinka CE wyznacz jako różnicę długości odcinków AC i AE. Ułóż równanie wynikające z twierdzenia Pitagorasa dla trójkąta OEC, otrzymując równanie, z którego wyznacz następnie promień okręgu.

Ćwiczenie 1
177Ćwiczenie 2
178Ćwiczenie 14
182Zadanie 2
187Zadanie 3
187Zadanie 7
187Ćwiczenie 6
192Zadanie 2
193Zadanie 5
193Ćwiczenie 1
197Zadanie 1
199Zadanie 9
200Zadanie 11
200Zadanie 1
208Zadanie 2
208Zadanie 3
208Zadanie 4
208Zadanie 6
209Zadanie 3
221Zadanie 4
221Zadanie 5
221Zadanie 7
221Zadanie 8
221Zadanie 9
222Ćwiczenie 4
226Zadanie 3
227Zadanie 4
227Zadanie 9
227Zadanie 10
227Zadanie 12
227Ćwiczenie 2
228Ćwiczenie 4
231Zadanie 6
234Zadanie 7
234Zadanie 9
235Zadanie 11
235Zadanie 12
235Zadanie 17
235Zadanie 13
237Zadanie 18
238Zadanie 20
238Zadanie 26
238Zadanie 27
238Zadanie 31
239Zadanie 33
239Zadanie 36
239Zadanie 38
239
