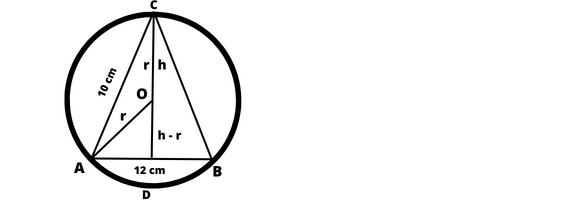
W tym zadaniu musisz obliczyć odległość środka okręgu opisanego na trójkącie równoramiennym od podstawy trójkąta.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Na początku sprawdź czy trójkąt jest ostrokątny, czy rozwartokątny. Aby to zrobić oceń, czy suma kwadratów długości ramion jest większa (trójkąt ostrokątny), czy mniejsza (trójkąt rozwartokątny) od kwadratu długości podstawy.
Następnie ułóż twierdzenie Pitagorasa dla trójkąta ADC, dzięki któremu możesz obliczyć długość wysokości trójkąta. Ułóż kolejne twierdzenie Pitagorasa – tym razem dla trójkąta ADO – jego przeciwprostokątna równa jest promieniowi okręgu, a przyprostokątna OD różnicy wysokości trójkąta i promienia okręgu. Z otrzymanego równania wyznacz długość promienia opisanego na trójkącie.
Długość szukanego odcinka |OD| jest równa różnicy wysokości trójkąta i promienia okręgu.

Ćwiczenie 1
177Ćwiczenie 2
178Ćwiczenie 14
182Zadanie 2
187Zadanie 3
187Zadanie 7
187Ćwiczenie 6
192Zadanie 2
193Zadanie 5
193Ćwiczenie 1
197Zadanie 1
199Zadanie 9
200Zadanie 11
200Zadanie 1
208Zadanie 2
208Zadanie 3
208Zadanie 4
208Zadanie 6
209Zadanie 3
221Zadanie 4
221Zadanie 5
221Zadanie 7
221Zadanie 8
221Zadanie 9
222Ćwiczenie 4
226Zadanie 3
227Zadanie 4
227Zadanie 9
227Zadanie 10
227Zadanie 12
227Ćwiczenie 2
228Ćwiczenie 4
231Zadanie 6
234Zadanie 7
234Zadanie 9
235Zadanie 11
235Zadanie 12
235Zadanie 17
235Zadanie 13
237Zadanie 18
238Zadanie 20
238Zadanie 26
238Zadanie 27
238Zadanie 31
239Zadanie 33
239Zadanie 36
239Zadanie 38
239
