W tym zadaniu musisz sformułować twierdzenie o środkowych w trójkącie, odpowiedzieć na pytania i oblicz podane odległości.
Twierdzenie o środkowych w trójkącie:
Środkowe w trójkącie przecinają się w jednym punkcie i punkt ten dzieli środkowe w stosunku 2 : 1 licząc od wierzchołków trójkąta.
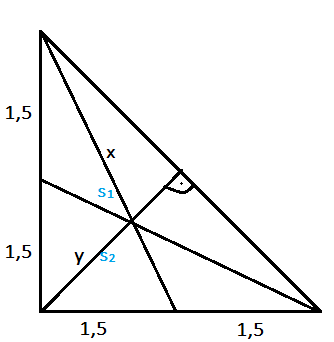
s1 – długość środkowej wychodzącej z wierzchołka kąta ostrego
s2 – długość środkowej wychodzącej z wierzchołka kąta prostego
c – przeciwprostokątna trójkąta
x – odległość punktu przecięcia środkowych od wierzchołka kąta ostrego
y – odległość punktu przecięcia środkowych od wierzchołka kąta prostego
![]()
![]()
![]()
![]()
![]()
Punkt przecięcia środkowych w trójkącie prostokątnym nie jest równo odległy od wszystkich wierzchołków trójkąta.

Aby obliczyć długość środkowej wychodzącej z wierzchołka kąta prostego zauważ, że dzieli ona trójkąt na dwa trójkąty prostokątne równoramienne, których długość ramienia jest równa długości przeciwprostokątnej dużego trójkąta. Następnie oblicz odległość wierzchołka kąta prostego od punktu przecięcia środkowych jako ![]()
Długość drugiej środkowej (trójkąt jest równoramienny, więc środkowe wychodzące z wierzchołków kątów ostrych mają równe długości) oblicz, korzystając z twierdzenia Pitagorasa. Wyznaczona odległość wierzchołka kąta ostrego od punktu przecięcia środkowych różni się od odpowiadającej jej odległości dla wierzchołka kąta prostego.

Ćwiczenie 1
177Ćwiczenie 2
178Ćwiczenie 14
182Zadanie 2
187Zadanie 3
187Zadanie 7
187Ćwiczenie 6
192Zadanie 2
193Zadanie 5
193Ćwiczenie 1
197Zadanie 1
199Zadanie 9
200Zadanie 11
200Zadanie 1
208Zadanie 2
208Zadanie 3
208Zadanie 4
208Zadanie 6
209Zadanie 3
221Zadanie 4
221Zadanie 5
221Zadanie 7
221Zadanie 8
221Zadanie 9
222Ćwiczenie 4
226Zadanie 3
227Zadanie 4
227Zadanie 9
227Zadanie 10
227Zadanie 12
227Ćwiczenie 2
228Ćwiczenie 4
231Zadanie 6
234Zadanie 7
234Zadanie 9
235Zadanie 11
235Zadanie 12
235Zadanie 17
235Zadanie 13
237Zadanie 18
238Zadanie 20
238Zadanie 26
238Zadanie 27
238Zadanie 31
239Zadanie 33
239Zadanie 36
239Zadanie 38
239
