W tym zadaniu musisz poprowadzić OP i wykaż prawdziwość twierdzenia.
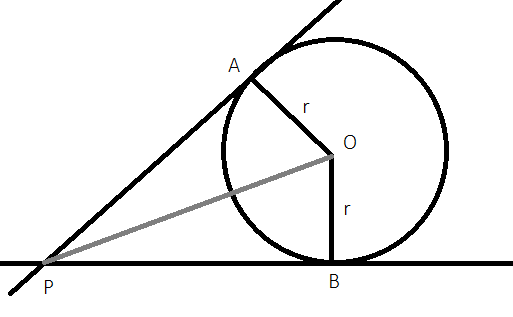
Trójkąty PBO oraz PAO są prostokątne, ponieważ promień poprowadzony do punktu styczności tworzy ze styczną kąt prosty. Mają one również dwie pary wspólnych boków, a więc i trzeci bok jest równej długości (co wynika np. z twierdzenia Pitagorasa).
![]()
Cnw.

Twierdzenie o odcinkach stycznych mówi, że odcinki dwóch stycznych poprowadzonych do okręgu z punktu, którego odległość od środka okręgu jest większa niż promień – wyznaczone przez ten punkt i odpowiednie punkty styczności – mają te same długości. Zatem, aby je udowodnić, musisz wykazać równość długości odcinków |PA| i |PB|. By to zrobić skorzystaj z przystawania trójkątów ABO i PAO (trójkąty mają równe kąty oraz wspólny bok).

Ćwiczenie 1
177Ćwiczenie 2
178Ćwiczenie 14
182Zadanie 2
187Zadanie 3
187Zadanie 7
187Ćwiczenie 6
192Zadanie 2
193Zadanie 5
193Ćwiczenie 1
197Zadanie 1
199Zadanie 9
200Zadanie 11
200Zadanie 1
208Zadanie 2
208Zadanie 3
208Zadanie 4
208Zadanie 6
209Zadanie 3
221Zadanie 4
221Zadanie 5
221Zadanie 7
221Zadanie 8
221Zadanie 9
222Ćwiczenie 4
226Zadanie 3
227Zadanie 4
227Zadanie 9
227Zadanie 10
227Zadanie 12
227Ćwiczenie 2
228Ćwiczenie 4
231Zadanie 6
234Zadanie 7
234Zadanie 9
235Zadanie 11
235Zadanie 12
235Zadanie 17
235Zadanie 13
237Zadanie 18
238Zadanie 20
238Zadanie 26
238Zadanie 27
238Zadanie 31
239Zadanie 33
239Zadanie 36
239Zadanie 38
239
