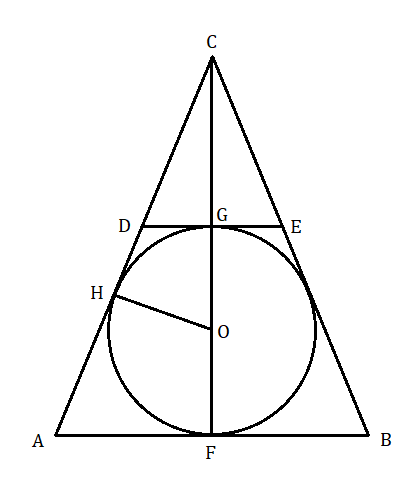
W tym zadaniu musisz podać długość odcinka DE.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Wyznacz wysokość CF trójkąta ABC korzystając z twierdzenia Pitagorasa. Następnie, korzystając z twierdzenia o odcinkach stycznych, wyznacz długość odcinka CH. Zauważ, że trójkąty AFC i OHC są podobne – są to trójkąty prostokątne o wspólnym kącie ostrym. Przyrównaj do siebie długości odpowiadających sobie długości boków w trójkątach, wyznaczając w ten sposób równanie, dzięki któremu możesz obliczyć promień okręgu. Trójkąty DEC i ABC również są podobne (DE || AB), skąd możesz utworzyć kolejne równanie stosunków – tym razem pozwalające na wyznaczenie długości odcinka |DE| (wcześniej oblicz jeszcze długości odcinka CG jako różnicę wysokości trójkąta i dwóch promieni).

Ćwiczenie 1
177Ćwiczenie 2
178Ćwiczenie 14
182Zadanie 2
187Zadanie 3
187Zadanie 7
187Ćwiczenie 6
192Zadanie 2
193Zadanie 5
193Ćwiczenie 1
197Zadanie 1
199Zadanie 9
200Zadanie 11
200Zadanie 1
208Zadanie 2
208Zadanie 3
208Zadanie 4
208Zadanie 6
209Zadanie 3
221Zadanie 4
221Zadanie 5
221Zadanie 7
221Zadanie 8
221Zadanie 9
222Ćwiczenie 4
226Zadanie 3
227Zadanie 4
227Zadanie 9
227Zadanie 10
227Zadanie 12
227Ćwiczenie 2
228Ćwiczenie 4
231Zadanie 6
234Zadanie 7
234Zadanie 9
235Zadanie 11
235Zadanie 12
235Zadanie 17
235Zadanie 13
237Zadanie 18
238Zadanie 20
238Zadanie 26
238Zadanie 27
238Zadanie 31
239Zadanie 33
239Zadanie 36
239Zadanie 38
239
