W tym zadaniu musisz sprawdzić, czy trójkąt o danych długościach boków jest trójkątem ostrokątnym, czy rozwartokątnym. Następnie oblicz promień okręgu opisanego na tym trójkącie.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Aby sprawdzić czy trójkąt jest ostrokątny, czy rozwartokątny oceń, czy suma kwadratów długości ramion jest większa (trójkąt ostrokątny), czy mniejsza (trójkąt rozwartokątny) od kwadratu długości podstawy.
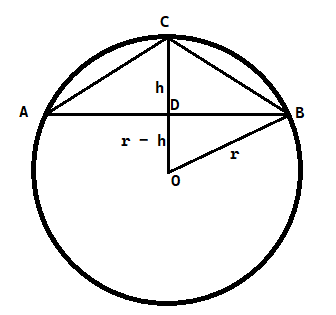
Narysuj rysunek pomocniczy, z którego odczytaj, że trójkąty CDB i ODB są prostokątne. Ułóż twierdzenie Pitagorasa dla trójkąta CDB i z jego pomocą wyznacz wysokość h trójkąta ABC. Następnie ułóż twierdzenie Pitagorasa dla trójkąta ODB, w którym przeciwprostokątna równa jest promieniowy okręgu, a przyprostokątna OD różnicy promienia okręgu i wysokości trójkąta. Z otrzymanego równania wyznacz długość promienia okręgu.

Ćwiczenie 1
177Ćwiczenie 2
178Ćwiczenie 14
182Zadanie 2
187Zadanie 3
187Zadanie 7
187Ćwiczenie 6
192Zadanie 2
193Zadanie 5
193Ćwiczenie 1
197Zadanie 1
199Zadanie 9
200Zadanie 11
200Zadanie 1
208Zadanie 2
208Zadanie 3
208Zadanie 4
208Zadanie 6
209Zadanie 3
221Zadanie 4
221Zadanie 5
221Zadanie 7
221Zadanie 8
221Zadanie 9
222Ćwiczenie 4
226Zadanie 3
227Zadanie 4
227Zadanie 9
227Zadanie 10
227Zadanie 12
227Ćwiczenie 2
228Ćwiczenie 4
231Zadanie 6
234Zadanie 7
234Zadanie 9
235Zadanie 11
235Zadanie 12
235Zadanie 17
235Zadanie 13
237Zadanie 18
238Zadanie 20
238Zadanie 26
238Zadanie 27
238Zadanie 31
239Zadanie 33
239Zadanie 36
239Zadanie 38
239
