W tym zadaniu musisz wyznaczyć wartość tangensa kąta, który jest ostry w równoległoboku, w którym długość boków wynosi 6 oraz 4 cm, zaś jedna z przekątnych jest długości 8cm.
Z twierdzenia cosinusów zastosowanego do trójkąta składającego się z boków równoległoboku oraz jego przekątnej (kąt α jest kątem naprzeciwko przekątnej, a więc kątem między bokami równoległoboku):
![]()
![]()
![]()
![]()
![]()
Niech kąt ostry w tym równoległoboku będzie oznaczony przez β. Wtedy β = 180° – α
![]()
Więc cosinus szukanego kąta wynosi ![]()
![]()
![]()
![]()
![]()
![]()
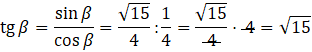
Odpowiedź: A. ![]()

Boki, których długości zostały podane oraz podana przekątna tworzą trójkąt. Nie jesteś w stanie określić czy podana przekątna jest dłuższą, czy krótszą przekątną, ale niezależnie od tego jesteś w stanie wyznaczyć tangensa kąta ostrego tego równoległoboku.
Niezależnie od tego, czy podana przekątna jest przekątną dłuższą czy krótszą, kąt będący kątem tego równoległoboku (niekoniecznie ostrym!) będzie leżał naprzeciw tej przekątnej. Aby wyznaczyć wartość cosinusa tego kąta możesz skorzystać z twierdzenia cosinusów. Ponieważ interesuje cię wartość cosinusa kąta leżącego naprzeciw przekątnej, to długość tej przekątnej musi znaleźć się po lewej stronie równania z twierdzenie cosinusów. Podstawiając długości boków i przekątnej otrzymasz:
![]()
![]()
![]()
![]()
Kąt α może być albo kątem ostrym, albo rozwartym. Jednakże, cosinusy kątów rozwartych są ujemne, co oznacza, że jest to cosinus kąta rozwartego. Kąt ostry w tym równoległoboku, oznaczony jako β ma więc miarę 180° – α. Korzystając ze wzoru redukcyjnego możesz zapisać:
![]()
Więc cosinus szukanego kąta wynosi ![]()
Tangens danego kąta to stosunek sinusa i cosinusa tego kąta. Jednakże nie znasz sinusa tego kąta. Możesz go obliczyć korzystając z jedynki trygonometrycznej.
![]()
![]()
![]()
![]()
Ponieważ β jest kątem ostrym to jego sinus musi być dodatni. Więc możesz odrzucić ujemny przypadek.
![]()
Teraz już możesz obliczyć tangens β.
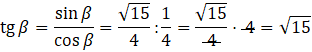

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
