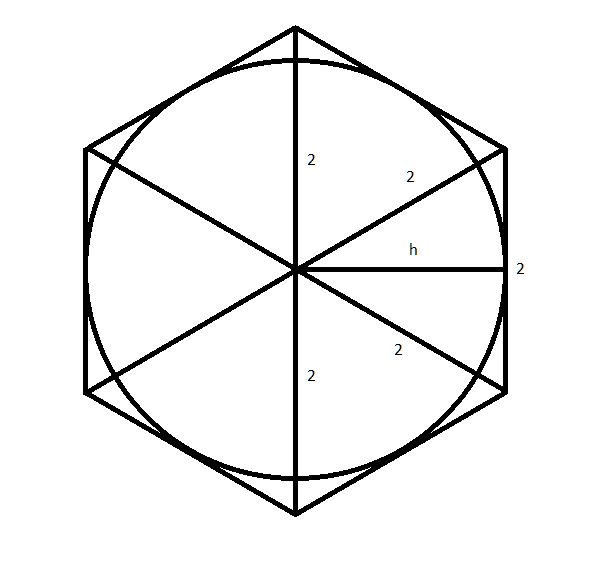
W tym zadaniu musisz wyznaczyć proporcję między polem koła wpisanego w pewien sześciokąt foremny, a polem tego sześciokąta, wiedząc, że dłuższe przekątne w tym sześciokącie są długości 4.
![]()
Gdzie r – promień okręgu wpisanego w sześciokąt, h – wysokość trójkąta równobocznego jednego „segmentu” sześciokąta.
![]()
![]()
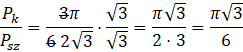
Odpowiedź: B. ![]()

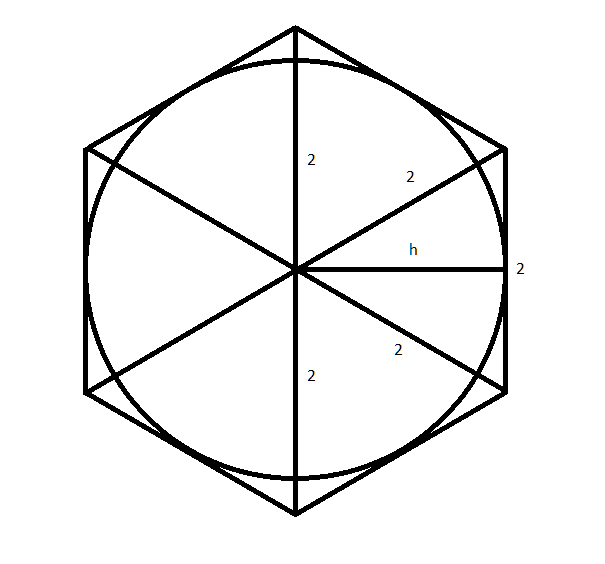
Zauważ, że sześciokąt foremny składa się z 6 trójkątów równobocznych. Dłuższe przekątne składają się z dwóch boków takich trójkątów równoramiennych. Skoro przekątna ta ma długość 4, to bok każdego z tych trójkątów ma długość 2.
Zauważ, że promień okręgu wpisanego w sześciokąt foremny to wysokość takiego trójkąta równobocznego. Więc długość promienia okręgu wpisanego wynosi:
![]()
Pole sześciokąta foremnego to po prostu sześć pól składowych trójkątów równobocznych.
![]()
Zaś pole koła wpisanego w ten sześciokąt wynosi:
![]()
Stosunek pola koła do pola sześciokąta obliczysz przez podzielenie pola koła przez pole sześciokąta:
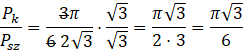

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
