W tym zadaniu musisz wyznaczyć stosunek pól trójkątów BCP i PDA, jeśli w prostokącie ABCD skonstruuje się okrąg mający średnicę w boku AB. Okrąg taki przetnie bok DC w dwóch miejscach. Punkt P oznaczamy punkt przecięcia się tego okręgu po stronie punktu D.

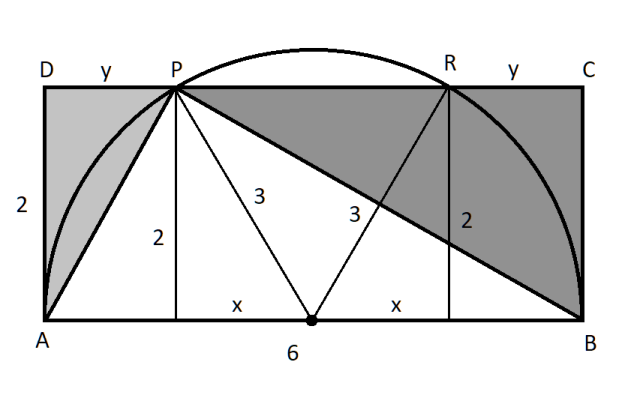
Odcinek łączący punkt P, ze środkiem okręgu, podobnie jak odcinek łączący środek okręgu z punktem R, to promień będący połową średnicy, której długość to 6.

$\text{[math]}$

y – przyprostokątna trójkąta PDA.

$\text{[math]}$

CP – przyprostokątna trójkąta BCP

$\text{[math]}$

Stosunek tych dwóch pól to:

$\text{[math]}$

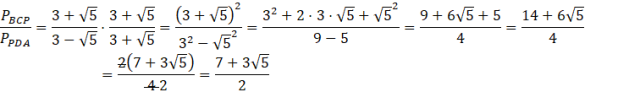
Przerysuj podany rysunek. Zauważ, że jeśli zaznaczysz wysokość białego trójkąta (która jest długością krótszego boku prostokąta) oraz zaznaczysz promień okręgu (którego długość wynosi 3, gdyż to połowa średnicy okręgu mającej długość 6, czyli dłuższego boku prostokąta) otrzymasz trójkąt prostokątny. Oznacz jego drugą przyprostokątną jako x. Wartość x możesz obliczyć z twierdzenia Pitagorasa.

$\text{[math]}$

Oczywiście x nie może być ujemny, więc możesz odrzucić ujemne rozwiązanie.

$\text{[math]}$

Zauważ, że po drugiej stronie można skonstruować symetryczny trójkąt. Jeśli oznaczysz drugi punkt przecięcia się okręgu z bokiem CD jako R, to odcinek PR ma długość 2x, czyli $\text{[math]}$ .

Odcinki DP oraz CR mają taką samą długość, którą oznacz jako y. Oczywiście cały odcinek CD składa się z dwóch odcinków y oraz odcinka PR, co możesz zapisać jako:

$\text{[math]}$

Oczywiście |CD| = 6. Podstawiając obliczoną wartość odcinka PR otrzymasz:

$\text{[math]}$

Odcinek y jest jedną z przyprostokątnych trójkąta PDA. Jego drugą przyprostokątną jest odcinek AD, którego długość wynosi 2. Więc pole trójkąta PDA to:

$\text{[math]}$

Przyprostokątną trójkąta BCP jest odcinek CP. Składa się on z odcinków CR (którego długość to y) oraz PR, co możesz zapisać jako:

$\text{[math]}$

Podstawiając wartości tych odcinków otrzymasz:

$\text{[math]}$

Drugą przyprostokątną trójkąta BCP jest odcinek BC o długości 2. Więc pole tego trójkąta wynosi:

$\text{[math]}$

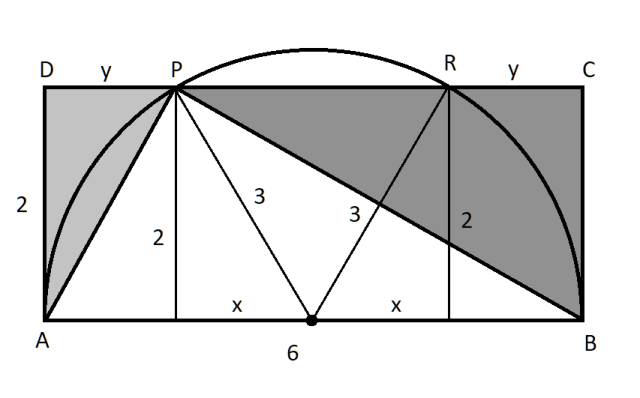
Stosunek tych dwóch pól to:

$\text{[math]}$

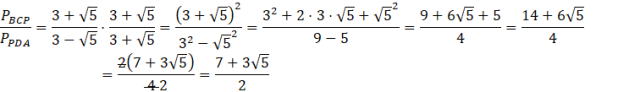
Ponieważ w mianowniku pojawił się pierwiastek musisz usunąć niewymierność z mianownika. Ponieważ jest to wyrażenie z pierwiastkiem zrób to przez przemnożenie licznika i mianownika przez to wyrażenie, ale ze zmienionym na przeciwny znakiem między liczbą a pierwiastkiem. Otrzymasz wtedy w mianowniku wzór skróconego mnożenia na różnicę kwadratów, który pozwoli pozbyć się pierwiastka z mianownika. W liczniku z kolei dostaniesz mnożenie dwóch takich samych nawiasów, które zapisać możesz jako podniesienie tego nawiasu do kwadratu. Aby obliczyć licznik, skorzystaj ze wzoru skróconego mnożenia na kwadrat sumy. Na koniec zauważ, że możesz wyciągnąć z licznika 2 przed nawias i skrócić z mianownikiem.

Matematyka z Plusem. Klasa 4. Podręcznik – rozwiązania i odpowiedzi

Zadanie 21. - strona 125

Zadanie

W tym zadaniu musisz wyznaczyć stosunek pól trójkątów BCP i PDA, jeśli w prostokącie ABCD skonstruuje się okrąg mający średnicę w boku AB. Okrąg taki przetnie bok DC w dwóch miejscach. Punkt P oznaczamy punkt przecięcia się tego okręgu po stronie punktu D.

Rozwiązanie

Wyjaśnienie

Matematyka - wybrane pytania