W tym zadaniu musisz określić jakie są rozwiązania równań ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
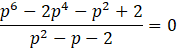
![]()
![]()
![]()
![]()
![]()
![]()
Równanie to zostało wcześniej rozwiązane i jego rozwiązaniami są:
![]()
![]()

Zauważ, że licznik wyrażenia w drugim równaniu, to wielomian z pierwszego równania. Zauważ także, że drugie równanie to ułamek przyrównany do 0, więc jego rozwiązanie będzie polegało na przyrównaniu licznika do zera (gdyż gdy wiesz, że ułamek wynosi 0, to jego licznik musi być zerem. Więc tak naprawdę drugie równanie sprowadzi się do rozwiązania pierwszego równania. Jednakże, ponieważ drugie równanie jest w postaci ułamka, gdzie zmienna występuje w mianowniku, musisz obliczyć dziedzinę i sprawdzić czy otrzymane rozwiązania należą do niej.
![]()
Zauważ, że wyciągając z pierwszych dwóch składników -p4 przed nawias otrzymasz w nawiasie to samo wyrażenie co w dalszej części wielomianu.
![]()
Teraz możesz wyciągnąć nawias przed nawias:
![]()
Otrzymałeś iloczyn przyrównany do 0, więc któryś z jego składników będzie wynosił 0.
![]()
![]()
Pamiętaj, że pierwiastkując obie strony pierwiastkami o parzystym stopniu musisz rozważyć po dwa przypadki:
![]()
Więc rozwiązaniami pierwszego równania będą:
![]()
Tak jak zostało to wyżej wspomniane, do rozwiązania tego samego równania sprowadza się rozwiązanie drugiego równania. Jednakże musisz jeszcze obliczyć dziedzinę tego równania.
![]()
Potraktuj to jako zwykłe równanie kwadratowe.
![]()
![]()
![]()
![]()
Teraz musisz odrzucić z rozwiązań drugiego równania liczby, które nie należą do jego dziedziny.
![]()
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
